Automation in Process Control 4th Module

ANALOG CONTROLLERS:

Modern implementation of controller action is provided by computers using software to perform the required math operations. Prior to the widespread use of computers, analog electronic circuits and pneumatic systems provided controller action. Some control system implementations still use analog electronics for special purposes and there remains a vast array of equipment in continued use in the process industry

General features

An analog controller is a device that implements the controller modes described previously, using analog signals to represent the loop parameters. The analog signal may be in the form of an electric current or a pneumatic air pressure. The controller accepts a measurement expressed in terms of one of these signals, calculates an output for the mode being used, and outputs an analog signal of the same type. Because the controller does solve equations, we think of it as an analog computer. The controller must be able to add, subtract, multiply, integrate, and find derivatives. It does this by working with analog voltages or pressures.

Typical Physical Layout

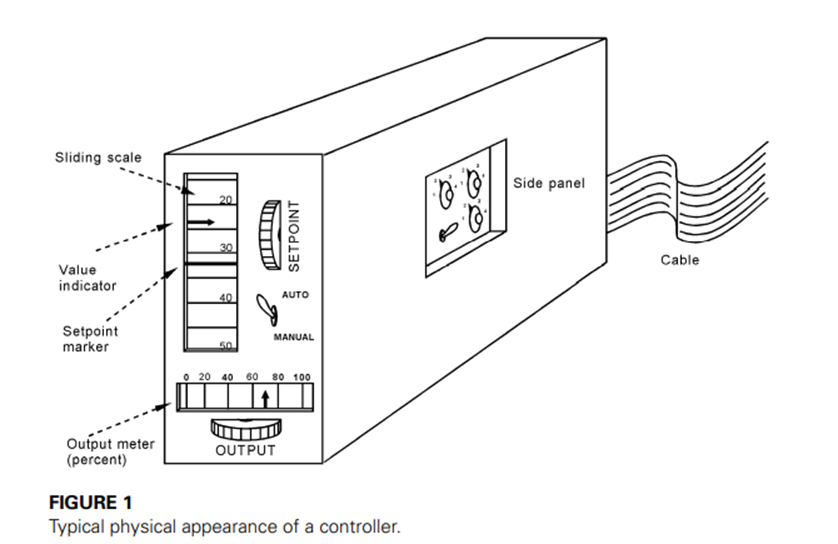
Analog controllers are usually designed to fit into a panel assembly as a slide in/out module, as shown in Figure 1. The front displays all necessary information and provides adjustment capability for the operator. When the unit is pulled out partway but still connected, other, less frequently required adjustments are available. When the controller is pulled still further out, an extension cable can be disconnected and the entire unit removed from the panel for replacement, if necessary.

Front Panel

The front panel of an analog controller displays information for operators and allows adjustment of the setpoint. Figure 1 shows a typical front panel. The setpoint knob moves a sliding scale under the fixed setpoint indicator. Thus, a fixed span of measurement above and below the setpoint is visible, as indicated by the measurement-value indicator.

The error is the difference between the setpoint indicator and the measurement meter. The display is typically expressed in percentage of span (4 to 20 mA or 3 to 15 psi). The lower meter shows the controller output, again expressed in percentage of span. Of course, the output is actually 4 to 20 mA or 3 to 15 psi, so that 0% would mean 4 mA,

for example. There is often a switch on the front panel by which the controller can be placed in a manual control, which means that the output can be adjusted independently of the input using the output-adjust knob. In automatic mode, this knob has no effect on the output. Connections to the controller are made through electrical or pneumatic cables connected to the rear of the unit.

Side Panel

On the side of the controller, when partially pulled out, knobs are available to adjust operation of the controller modes. On this panel, as shown in Figure 1, the proportional, integral (reset), and derivative (rate) gains can be adjusted. In addition, filtering action and reverse/direct operation can often be selected.

Electronic controllers

In the following treatment of electronic methods of realizing controller modes, emphasis is on the use of op amps as the primary circuit element. Discrete electronic components also are used to implement this function, but the basic principles are best illustrated using op amp circuits. Op amp circuits other than the ones described also can be developed

Error Detector

The detection of an error signal is accomplished in electronic controllers by taking the difference between voltages. One voltage is generated by the process signal current passed through a resistor. The second voltage represents the setpoint. This is usually generated by a voltage divider using a constant voltage as a source.

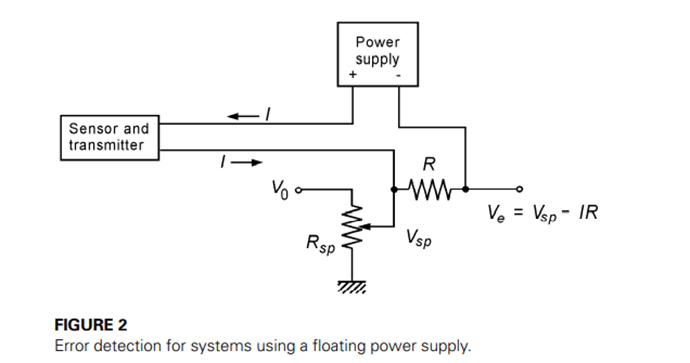
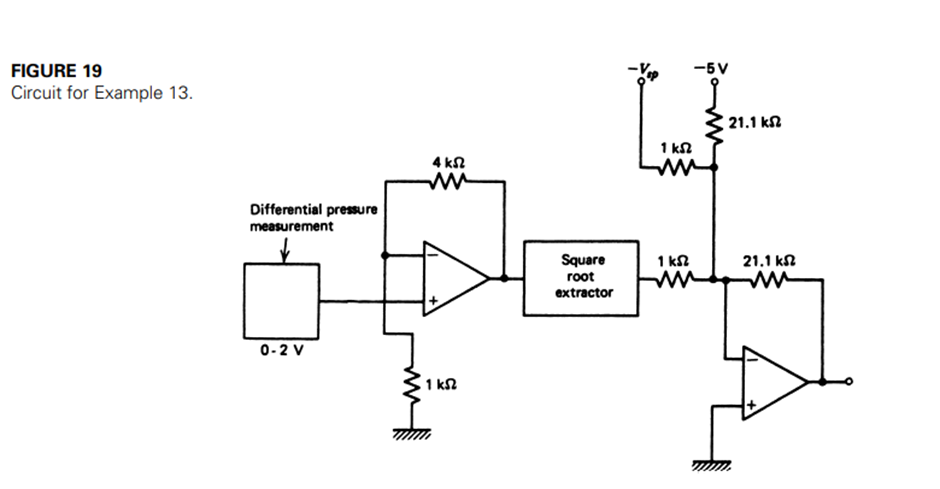
An example is shown in Figure 2. We assume a two-wire system is in use so that the current drawn from the floating power supply is the 4- to 20-mA signal current. The signal current is used to produce a voltage, IR, across the resistor, R. This is placed in series opposition to a voltage V_sp, tapped from a variable resistor, R_sp, connected to a constant positive source,V_o . The result is an error voltage, V_e = V_sp - IR. This is then used in the process controller to calculate controller output.

Single Mode

The following systems and op amp circuits illustrate methods of implementing the pure modes of controller action.

Two-Position

A two-position controller can be implemented by a great variety of electronic and electromechanical designs. In the past, many household air-conditioning and heating systems employed a two-position controller constructed from a bimetal strip and mercury switch, as shown in Figure 4. We see that as the bimetal strip bends because of a temperature decrease, it reaches a point where the mercury slides down to close an electrical contact.

The inertia of the mercury tends to keep the system in that position until the temperature increases to a value above the setpoint temperature. This provides the required neutral zone to prevent excessive cycling of the system

A method using op amp implementation of ON/OFF control with adjustable neutral zone is given in Figure 5. For this circuit, we assume that if the controller input voltage, V, reaches a value V_H, then the comparator output should go to the ON state, which is defined as some voltage, V_o. When the input voltage falls below a value, the comparator output should switch to the OFF state, which is defined as 0 V. The comparator output switches states when the voltage on its input, V₁, is equal to the setpoint value, V_sp. Analysis of this circuit shows that the high (ON) switch voltage is

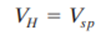
and the low (OFF) switching voltage is

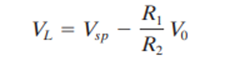
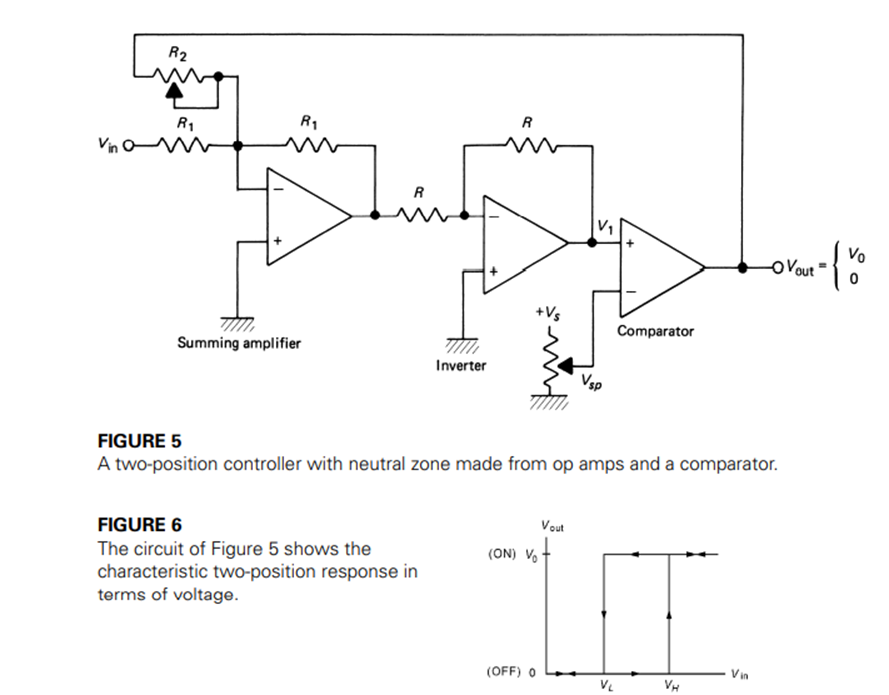
Figure 6 shows the typical two-position relationship between input and output voltage for this circuit.

(Explain any one of two method)

Proportional Mode

Proportional Mode

Implementation of this mode requires a circuit that has a response given by

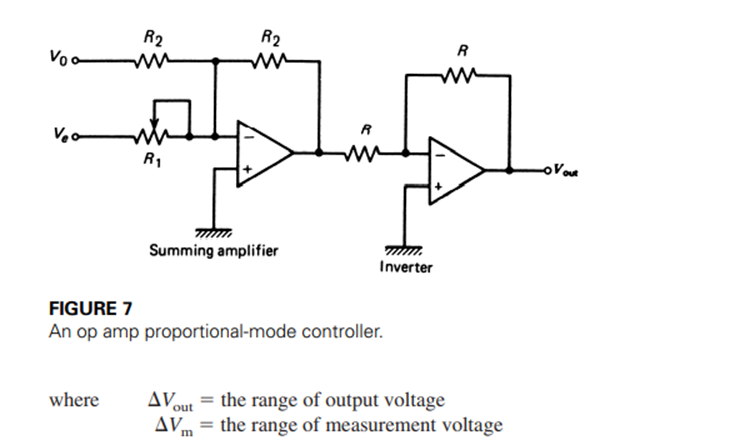
If we consider both the controller output and error to be expressed in terms of voltage, we see that Equation (14) is simply a summing amplifier. The op amp circuit in Figure 7 shows such an electronic proportional controller. In this case, the analog electronic equation for the output voltage is

The design of a proportional controller calls for specification of the proportional gain described by K_P in Equation (14) that expresses the percent of output for an error of 1% of the measurement range. Alternatively it could be described as the proportional band, PB = 100/KP.

This must now be expressed in terms of the voltage gain, G_p, in Equation (3). The relationship between G_P and K is given by,

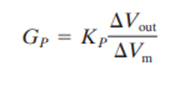
Integral Mode

Previously, we saw that the integral mode was characterized by an equation of the form

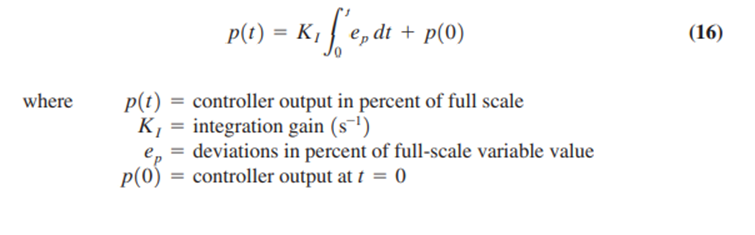
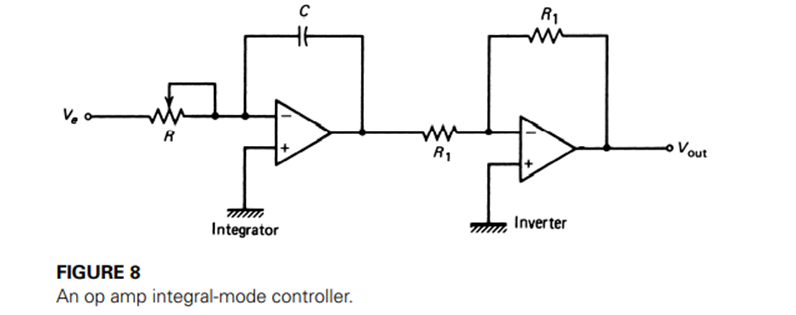
This function is easy to implement when op amps are used as the building blocks. A diagram of an integral controller is shown in Figure 8. The corresponding equation relating input to output is

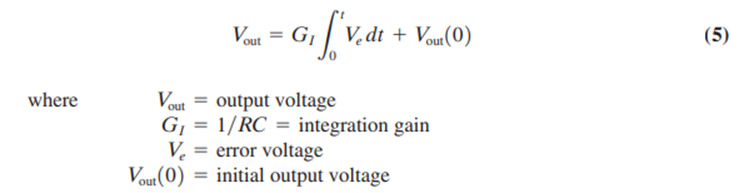
The values of R and C can be adjusted to obtain the desired integration time. The initial controller output is the integrator output at  t = 0. As we noted earlier, the integration time constant determines the rate at which controller output increases when the error is constant. If is made too large, the output rises so fast that overshoots of the optimum setting occur and cycling is produced.

The actual value of G₁, and therefore of R and C, is determined from K₁ and the input and output voltage ranges. One way to do this is to recognize that the integral gain says that an input error of 1% must produce an output that changes as K₁ percent per second. Another way is to know that if an error of 1% lasts for 1 s, the output must change by percent.

Derivative Mode

The derivative mode is never used alone because it cannot provide a controller output when the error is zero. Nevertheless, we show here how it is implemented with op amps so it can be combined with other modes. The control mode equation was given earlier as

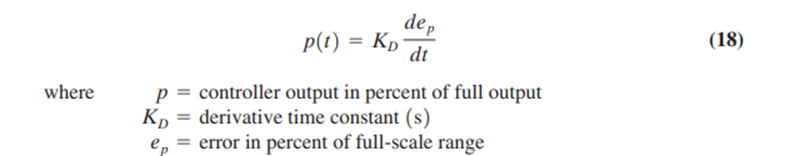
In principle, this mode could be implemented by the op amp circuit presented earlier. Indeed, the theoretical transfer function for this circuit given in Equation (6) looks just like Equation (9.18) with appropriate identifications in terms of circuit elements:

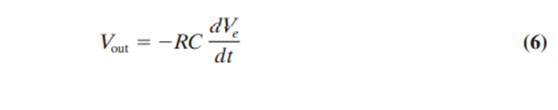
where the input voltage has been set equal to the controller error voltage.

From a practical perspective, this circuit cannot be used because it tends to be unstable; that is, it may begin to exhibit spontaneous oscillations in the output voltage. The reason for this instability is the very large gain at high frequencies where the derivative is very large

To study this effect, let us assume that the input voltage is given by a sinusoidal voltage oscillating with some frequency, f; then .

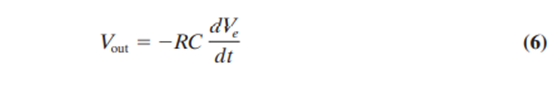
So, from Equation (6) we can write the amplitude of the output as,

This equation shows that the magnitude of the output voltage increases linearly with frequency. So, in principle, as the frequency goes to infinity, so does the output! Clearly this is unacceptable in our control system. A little high-frequency noise will cause large excursions in output voltage.

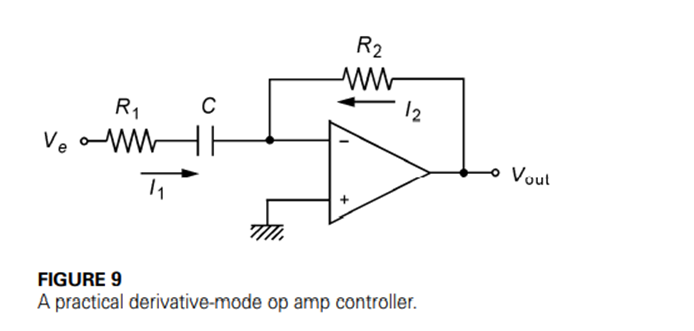
In order to make a practical circuit, a modification is provided that essentially “clamps” the gain above some frequency to a constant value. We make sure that the clamped frequencies are well above anything that could occur in the actual control system. This way, the circuit provides a derivative output in the frequencies of practical interest but simply acts like a fixed-gain amplifier at higher frequencies. Figure 9 shows that the simple modification is to place a resistor in series with the capacitor.

The actual transfer function for this circuit can be shown to be given by

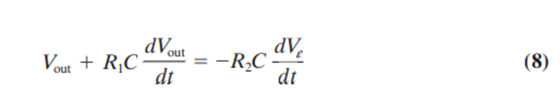
You can see that the output depends upon the derivative of the input voltage, but there is now an extra term involving the derivative of the output voltage. Essentially, we have a first-order differential equation relating input and output voltage

Composite Controller Modes

The combination of several controller modes was found to combine the advantages of each mode and, in some cases, eliminate disadvantages. Composite modes are implemented easily using op amp techniques. Basically, this consists of simply combining the mode circuits introduced in the previous section

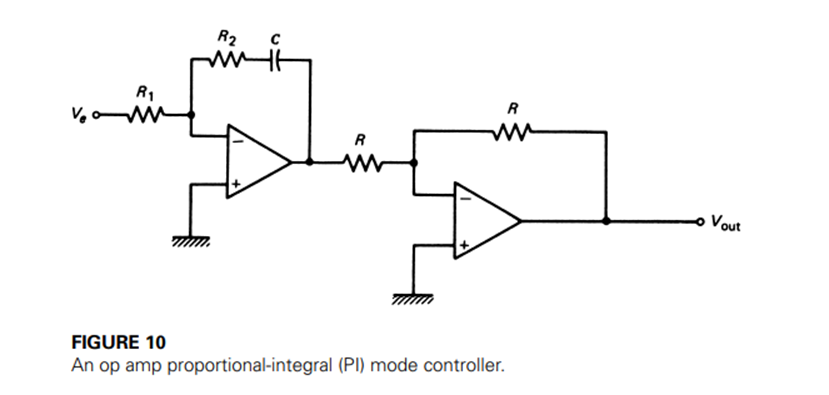
Proportional-Integral

A simple combination of the proportional and integral circuits provides the proportional-integral mode of controller action. The resulting circuit is shown in Figure 10. For this case, the relation between input and output is most easily found by applying op amp circuit analysis. We get (including the inverter)

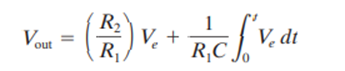
The definition of the proportional-integral controller mode includes the proportional gain in the integral term, so we write

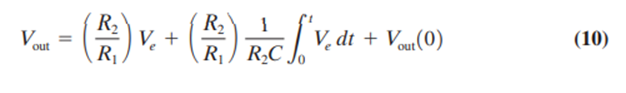
The adjustments of this controller are the proportional band through G_P = R₂/R₁, and the integration gain through G₁ = 1/R₂C

Proportional-Derivative

A powerful combination of controller modes is the proportional and derivative modes. This combination is implemented using a circuit similar to that shown in Figure 11. Analysis shows that this circuit responds according to the equation

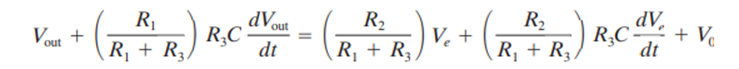
where the quantities are defined in the figure and the output inverter has been included.

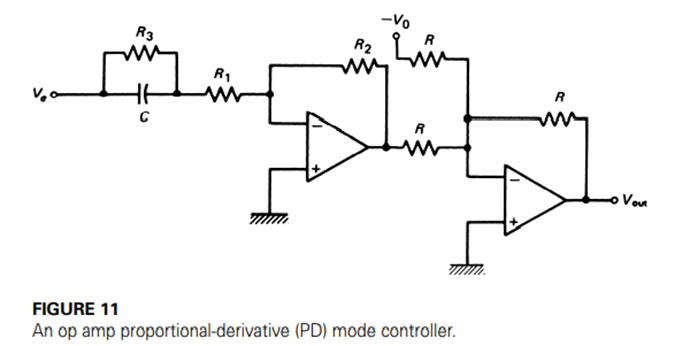
This circuit includes the clamp to protect against high gain at high frequency in the derivative term. In this case, the condition represented by Equation (9) is modified slightly to use an effective resistance given by

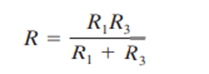
Then the condition becomes as usual, 2πf_maxRC = 0.1. Assuming this criterion has been met, the equation for the proportional-derivative response becomes

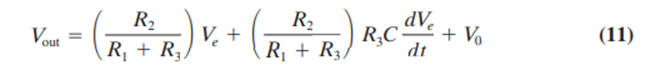
where the proportional gain is

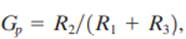
and the derivative gain is .

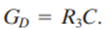
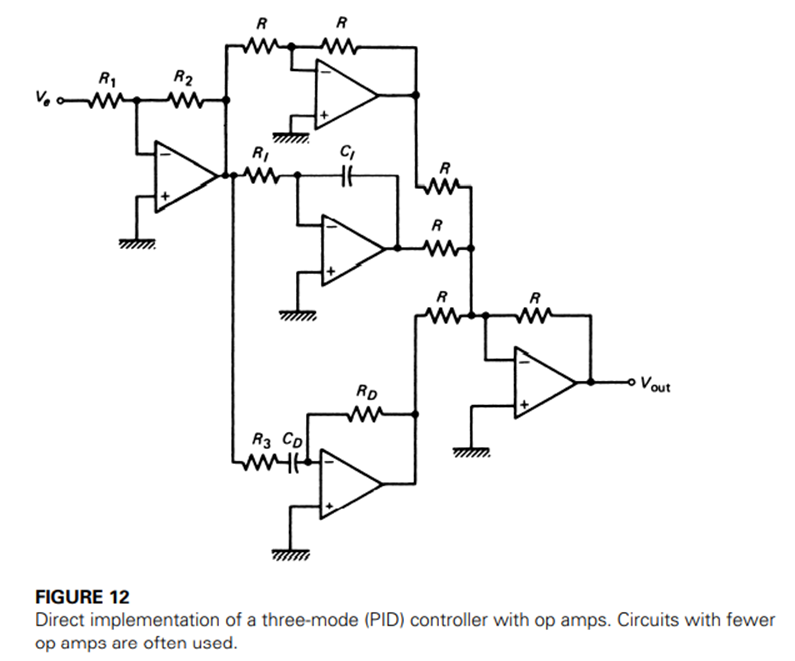
PID (Three-Mode) The ultimate process controller is the one that exhibits proportional, integral, and derivative response to the process-error input. This mode is characterized by the equation

The zero-error term of the proportional mode is not necessary because the integral automatically accommodates for offset and nominal setting. This mode can be provided by a straight application of op amp circuits, resulting in the circuit of Figure 12.

It must be noted, however, that it is possible to reduce the complexity of the circuitry of Figure 12 and still realize the three-mode action, but in these cases an interaction results between derivative and integral gains.

We will use the circuit of Figure 12 because it is easy to follow in illustrating the principles of implementing this mode. Analysis of the circuit shows that the output is

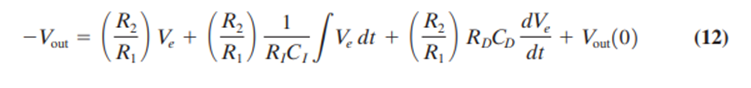
Pneumatic controllers

General Features

➢The outward appearance of a pneumatic controller is typically the same as that for the electronic controller. The same readout of setpoint, error, and controller output appears, and adjustments of gain, rate, and reset are available.

➢The working signal is most typically the 3- to 15-psi standard pneumatic process-ontrol signal, usually derived from a regulated air supply of 20 to 30 psi.

➢The pneumatic controller is based on the nozzle/flapper described previously as the basic mechanism of operation, much as the op amp is used in electronics.

Mode Implementation

Proportional

A proportional mode of operation can be achieved with the system shown in Figure 13. Operation is understood by noting that if the input pressure increases, then the input bellows forces the flapper to rotate to close off the nozzle. When this happens, the output pressure increases so that the feedback bellows exerts a force to balance that of the input bellows. A balance condition then occurs when torques exerted by each about the pivot are equal, or

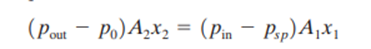
This equation is solved to find the output pressure

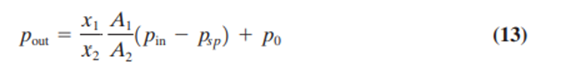
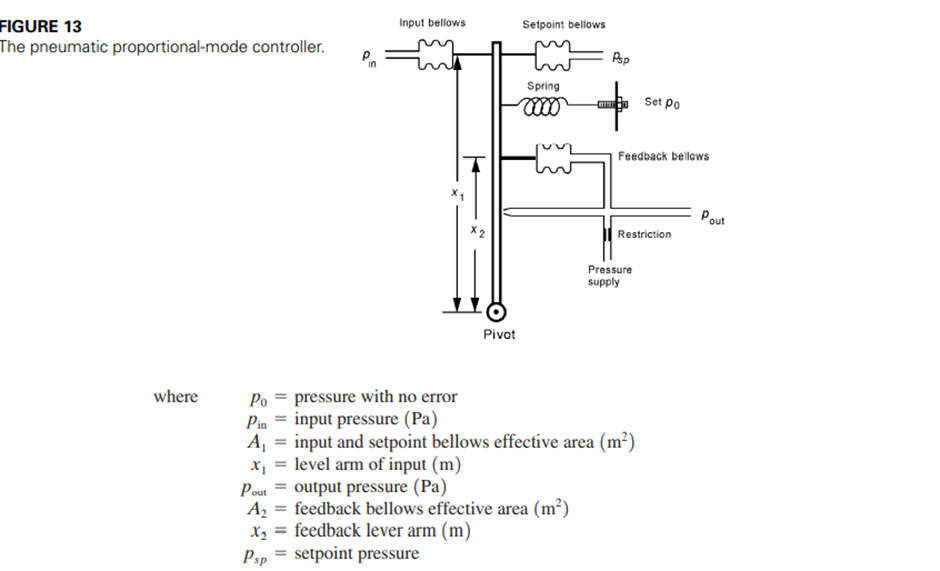
This relation is based on the notion of torque equaling force times lever arm, and the fact that a pressure in a bellows produces a force that is effectively the pressure times bellows area, much like a diaphragm. Equation (13) displays the standard response of a proportional mode in that output is directly proportional to input. The gain in this case is given by

Because the bellows are usually of fixed geometry, the gain is varied by changing the lever arm length. In this simple representation, the gain is established by the distance between the bellows. If this separation is changed, the forces are no longer balanced, and for the same pressure a new controller output will be formed, corresponding to the new gain.

Proportional-Integral

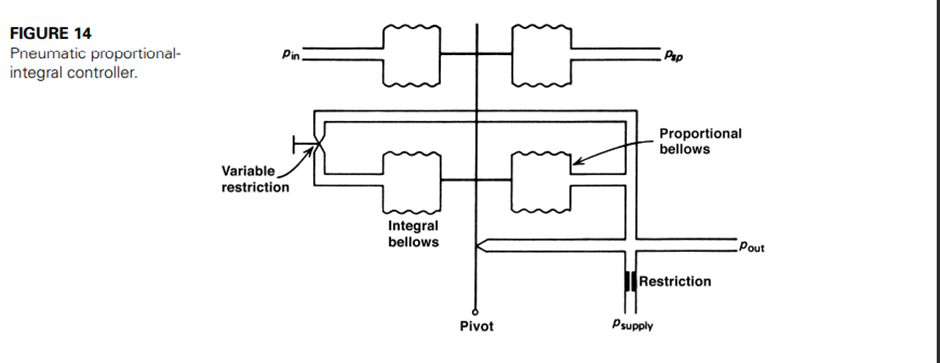
This control mode is also implemented using pneumatics by the system shown in Figure 14. In this case, an extra bellows with a variable restriction is added to the proportional system. Suppose the input pressure shows a sudden increase. This drives the flapper toward the nozzle, increasing output pressure until the proportional bellows balances the input as in the previous case.

The integral bellows is still at the original output pressure, because the restriction prevents pressure changes from being transmitted immediately.

As the increased pressure on the output bleeds through the restriction, the integral bellows slowly moves the flapper closer to the nozzle, thereby causing a steady increase in output pressure (as dictated by the integral mode). The variable restriction allows for variation of the leakage rate, and hence the integration time

Proportional-Derivative

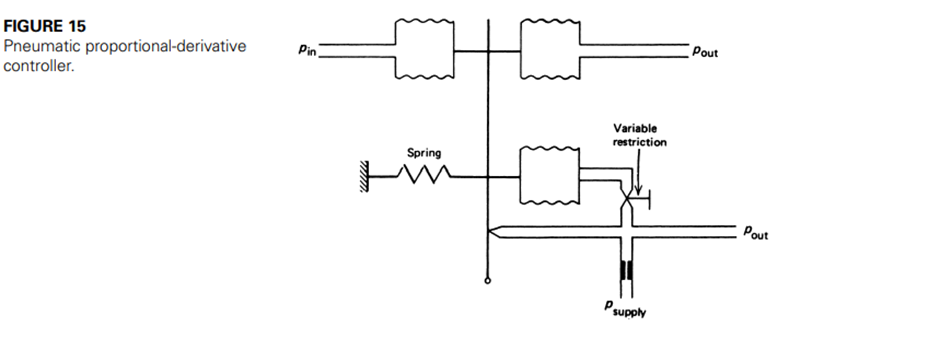
This controller action can be accomplished pneumatically by the method shown in Figure 15. A variable restriction is placed on the line leading to the balance bellows. Thus, as the input pressure increases, the flapper is moved toward the nozzle with no impedance, because the restrictions prevent an immediate response of the balance bellows. Thus, the output pressure rises very fast and then, as the increased pressure leaks into the balance bellows, decreases as the balance bellows moves the flapper back away from the nozzle. Adjustment of the variable restriction allows for changing the derivative time constraint.

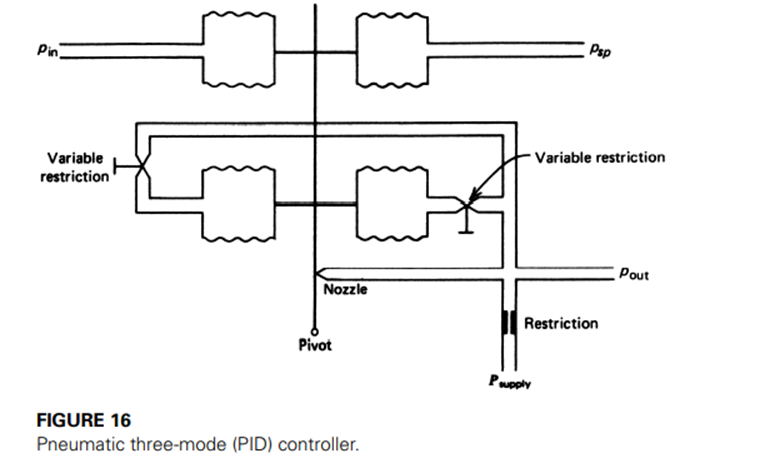
Three-Mode

The three-mode controller is actually the most common type produced, because it can be used to accomplish any of the previous modes by setting of restrictions. This device is shown in Figure 16, and, as can be seen, it is simply a combination of the three systems presented. By opening or closing restrictions, the three-mode controller can be used to implement the other composite modes. Proportional gain, reset time, and rate are set by adjustment of bellows separation and restriction size

Designs considerations

To illustrate some of the facets involved in setting up a process-control loop, it would be valuable to follow through some hypothetical examples. The following examples assume that a process-control loop is required, and that the controller operation must be provided by electronic analog circuits