Computer Organization 2nd Module
MODULE 2
ADDRESSING MODES
• The different ways in which the location of an operand is specified in an instruction are referred to as addressing modes.

1.11.1 IMPLEMENTATION OF VARIABLE AND CONSTANTS
• Variables & constants are the simplest data-types and are found in almost every computer program.
• In assembly language, a variable is represented by allocating a register (or memory-location) to hold its value. Thus, the value can be changed as needed using appropriate instructions.
❖ Register Mode
• The operand is the contents of a register.
• The name (or address) of the register is given in the instruction.
• Registers are used as temporary storage locations where the data in a register are accessed.
• For example, the instruction,
Move R1, R2 ;Copy content of register R1 into register R2
❖ Absolute (Direct) Mode
• The operand is in a memory-location.
• The address of memory-location is given explicitly in the instruction.
• For example, the instruction,
Move LOC, R2 ;Copy content of memory-location LOC into register R2.
❖ Immediate Mode
• The operand is given explicitly in the instruction.
• For example, the instruction,
Move #200, R0 ;Place the value 200 in register R0
• Clearly, the immediate mode is only used to specify the value of a source-operand.
1.11.2 INDIRECTION AND POINTERS
• In this case, the instruction does not give the operand or its address explicitly; instead, it provides information from which the memory-address of the operand can be determined. We refer to this address as the effective address(EA) of the operand.
❖ Indirect Mode
• The EA of the operand is the contents of a register(or memory-location) whose address appears in the instruction.
• The register (or memory-location) that contains the address of an operand is called a pointer. {The indirection is denoted by ( ) sign around the register or memory-location}.
E.g: Add (R1),R0;The operand is in memory. Register R1 gives the effective-address(B) of the operand. The data is read from location B and added to contents of register R0
* To execute the Add instruction in fig (a), the processor uses the value which is in register R1, as the EA of the operand.
* It requests a read operation from the memory to read the contents of location B. The value read is the desired operand, which the processor adds to the contents of register R0.
* Indirect addressing through a memory location is also possible as shown in fig (b). In this case, the processor first reads the contents of memory location A, then requests a second read operation using the value B as an address to obtain the operand
• In below program, Register R2 is used as a pointer to the numbers in the list, and the operands are accessed indirectly through R2.
• The initialization-section of the program loads the counter-value n from memory-location N into R1 and uses the immediate addressing-mode to place the address value NUM1, which is the address of the first number in the list, into R2. Then it clears R0 to 0.
• The first two instructions in the loop implement the unspecified instruction block starting at LOOP.
• The first time through the loop, the instruction Add (R2), R0 fetches the operand at location NUM1 and adds it to R0.
• The second Add instruction adds 4 to the contents of the pointer R2, so that it will contain the address value NUM2 when the above instruction is executed in the second pass through the loop.

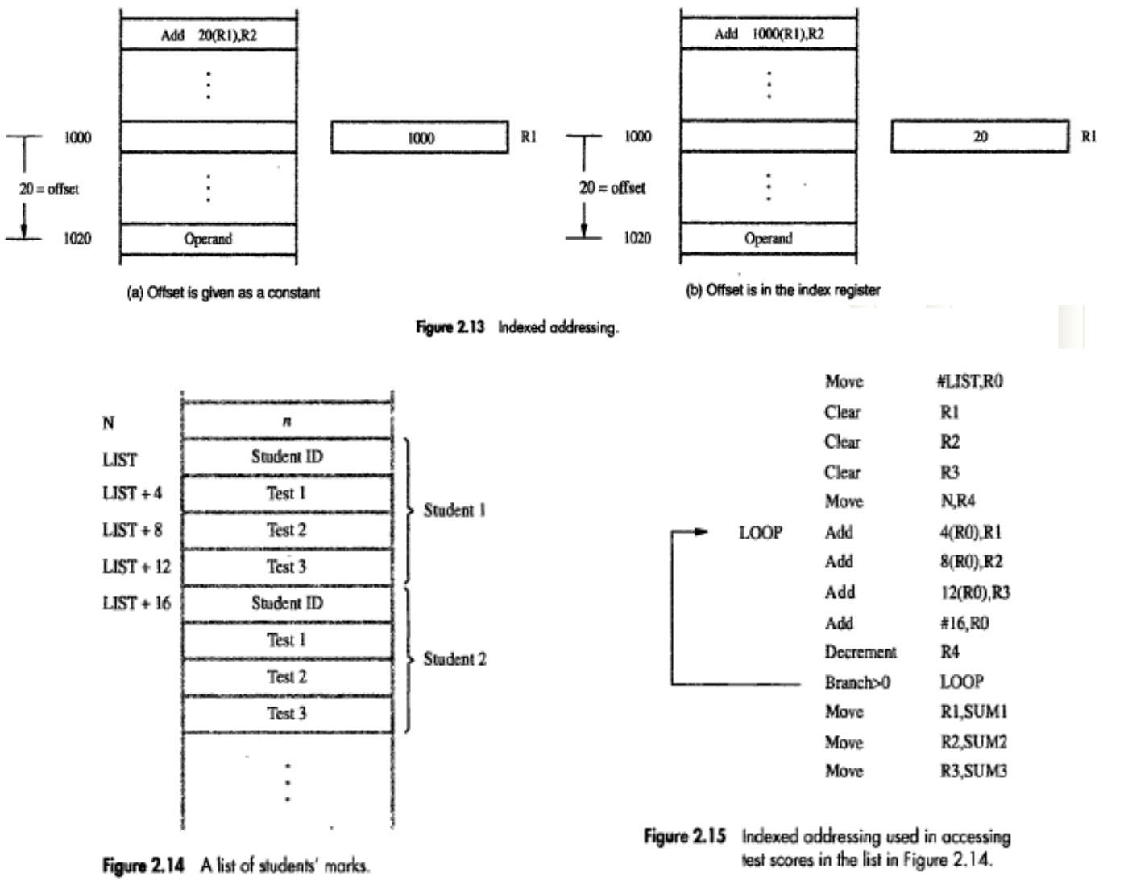
1.11.3 INDEXING AND ARRAYS
• A different kind of flexibility for accessing operands is useful in dealing with lists and arrays.
❖ Index mode
• The operation is indicated as X(Ri)
where X=the constant value contained in the instruction Ri=the name of the index register
• The effective-address of the operand is given by
EA=X+[Ri]
• The contents of the index-register are not changed in the process of generating the effective-address.
• In an assembly language program, the constant X may be given either
→ as an explicit number or
→ as a symbolic-name representing a numerical value.
* Fig (a) illustrates two ways of using the Index mode. In fig(a), the index register, R1, contains the address of a memory location, and the value X defines an offset(also called a displacement) from this address to the location where the operand is found.
* An alternative use is illustrated in fig (b). Here, the constant X corresponds to a memory address, and the contents of the index register define the offset to the operand. In either case, the effective address is the sum of two values; one is given explicitly in the instruction, and the other is stored in a register.
❖ Base with Index Mode
• Another version of the Index mode uses 2 registers which can be denoted as (Ri, Rj)
• Here, a second register may be used to contain the offset X.
• The second register is usually called the base register.
• The effective-address of the operand is given by
EA=[Ri]+[Rj]
• This form of indexed addressing provides more flexibility in accessing operands, because both components of the effective address can be changed.
❖ Base with Index & Offset Mode
• Another version of the Index mode uses 2 registers plus a constant, which can be denoted as X(Ri, Rj)
• The effective-address of the operand is given by
EA=X+[Ri]+[Rj]
• This added flexibility is useful in accessing multiple components inside each item in a record, where the beginning of an item is specified by the (Ri, Rj) part of the addressing-mode. In other words, this mode implements a 3-dimensional array.
1.11.4 RELATIVE MODE
• This is similar to index-mode with an exception: The effective address is determined using the PC in place of the general purpose register Ri.
• The operation is indicated as X(PC).
• X(PC) denotes an effective-address of the operand which is X locations above or below the current contents of PC.
• Since the addressed-location is identified "relative" to the PC, the name Relative mode is associated with this type of addressing.
• This mode is used commonly in conditional branch instructions.
• An instruction such as
Branch > 0 LOOP ;Causes program execution to go to the branch target location identified by name LOOP if branch condition is satisfied.
1.11.5 ADDITIONAL ADDRESSING MODES
• The following 2 modes are useful for accessing data items in successive locations in the memory.
❖ Auto-increment Mode
• The effective-address of operand is the contents of a register specified in the instruction (Fig: 2.16).
• After accessing the operand, the contents of this register are automatically incremented to point to the next item in a list.
• Implicitly, the increment amount is 1.
• This mode is denoted as
(Ri)+ ;where Ri=pointer register
❖ Auto-decrement Mode
• The contents of a register specified in the instruction are first automatically decremented and are then used as the effective address of the operand.
• This mode is denoted as
-(Ri) ;where Ri=pointer register
• These 2 modes can be used together to implement an important data structure called a stack.

1.12 ASSEMBLY LANGUAGE
• A complete set of symbolic names and rules for their use constitute an assembly language.
• The set of rules for using the mnemonics in the specification of complete instructions and programs is called the syntax of the language.
• Programs written in an assembly language can be automatically translated into a sequence of machine instructions by a program called an assembler.
• The user program in its original alphanumeric text formal is called a source program, and the assembled machine language program is called an object program.
• Move instruction is written is
MOVE R0,SUM ;The mnemonic MOVE represents the binary pattern, or OP code, for the operation performed by the instruction.
• The instruction
ADD #5,R3 ;Adds the number 5 to the contents of register R3 and puts the result back into register R3.
1.12.1 ASSEMBLER DIRECTIVES
• EQU informs the assembler about the value of an identifier (Figure: 2.18).
Ex: SUM EQU 200 ; This statement informs the assembler that the name SUM should be replaced by the value 200 wherever it appears in the program.
• ORIGIN tells the assembler about the starting-address of memory-area to place the data block.
• DATAWORD directive tells the assembler to load a value (say 100) into the location (say 204). Ex: N DATAWORD 100
• RESERVE directive declares that a memory-block of 400 bytes is to be reserved for data and that the name NUM1 is to be associated with address 208.
Ex: NUM1 RESERVE 400
• END directive tells the assembler that this is the end of the source-program text.
• RETURN directive identifies the point at which execution of the program should be terminated.
• Any statement that makes instructions or data being placed in a memory-location may be given a label.
• The label (say N or NUM1) is assigned a value equal to the address of that location.

1.12.2 GENERAL FORMAT OF A STATEMENT
• Most assembly languages require statements in a source program to be written in the form:
Label Operation Operands Comment
→ Label is an optional name associated with the memory-address where the machine language instruction produced from the statement will be loaded.
→ The Operation field contains the OP-code mnemonic of the desired instruction or assembler → The
Operand field contains addressing information for accessing one or more operands, depending on the type of instruction.
1.12.3 ASSEMBLY AND EXECUTION OF PRGRAMS
• Programs written in an assembly language are automatically translated into a sequence of machine instructions by the assembler.
• Assembler program
→ replaces all symbols denoting operations & addressing-modes with binary-codes used in machine instructions.
→ replaces all names and labels with their actual values.
→ assigns addresses to instructions & data blocks, starting at the address given in the ORIGIN directive.
→ inserts constants that may be given in DATAWORD directives.
→ reserves memory-space as requested by RESERVE directives.
• As the assembler scans through a source-program, it keeps track of all names of numerical-values that correspond to them in a symbol-table. Thus, when a name appears a second time, it is replaced with its value from the table. Hence, such an assembler is called a two-pass assembler.
• The assembler stores the object-program on a magnetic-disk. The object-program must be loaded into the memory of the computer before it is executed. For this, a loader program is used.
• Debugger program is used to help the user find the programming errors.
• Debugger program enables the user
→ to stop execution of the object-program at some points of interest and
→ to examine the contents of various processor registers and memory-location
→ The Comment field is used for documentation purposes to make the program easier to understand.
1.13 BASIC INPUT/OUTPUT OPERATIONS
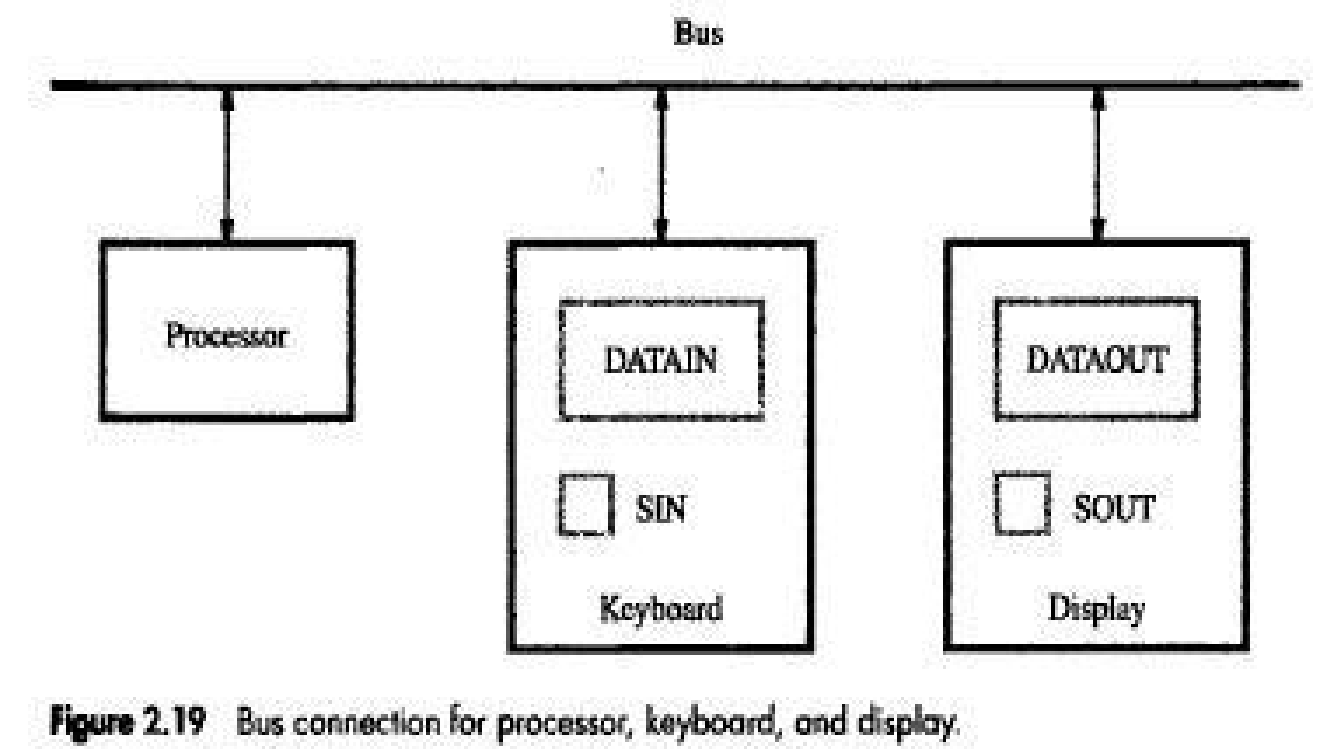
• Consider the problem of moving a character-code from the keyboard to the processor. For this transfer, buffer-register(DATAIN) & a status control flags(SIN) are used.
• Striking a key stores the corresponding character-code in an 8-bit buffer-register(DATAIN) associated with the keyboard (Figure: 2.19).
• To inform the processor that a valid character is in DATAIN, a SIN is set to 1.
• A program monitors SIN, and when SIN is set to 1, the processor reads the contents of DATAIN.
• When the character is transferred to the processor, SIN is automatically cleared to 0.
• If a second character is entered at the keyboard, SIN is again set to 1 and the process repeats.
• An analogous process takes place when characters are transferred from the processor to the display. A buffer-register, DATAOUT, and a status control flag, SOUT are used for this transfer.
• When SOUT=1, the display is ready to receive a character.
• The transfer of a character to DATAOUT clears SOUT to 0.
• The buffer registers DATAIN and DATAOUT and the status flags SIN and SOUT are part of circuitry commonly known as a device interface.
• Following is a program to read a line of characters and display it

MEMORY-MAPPED I/O
• Some address values are used to refer to peripheral device buffer-registers such as DATAIN and DATAOUT.
• No special instructions are needed to access the contents of the registers; data can be transferred between these registers and the processor using instructions such as Move, Load or Store.
• For example, contents of the keyboard character buffer DATAIN can be transferred to register R1 in the processor by the instruction
MoveByte DATAIN,R1
• The MoveByte operation code signifies that the operand size is a byte.
• The Testbit instruction tests the state of one bit in the destination, where the bit position to be tested is indicated by the first operand.
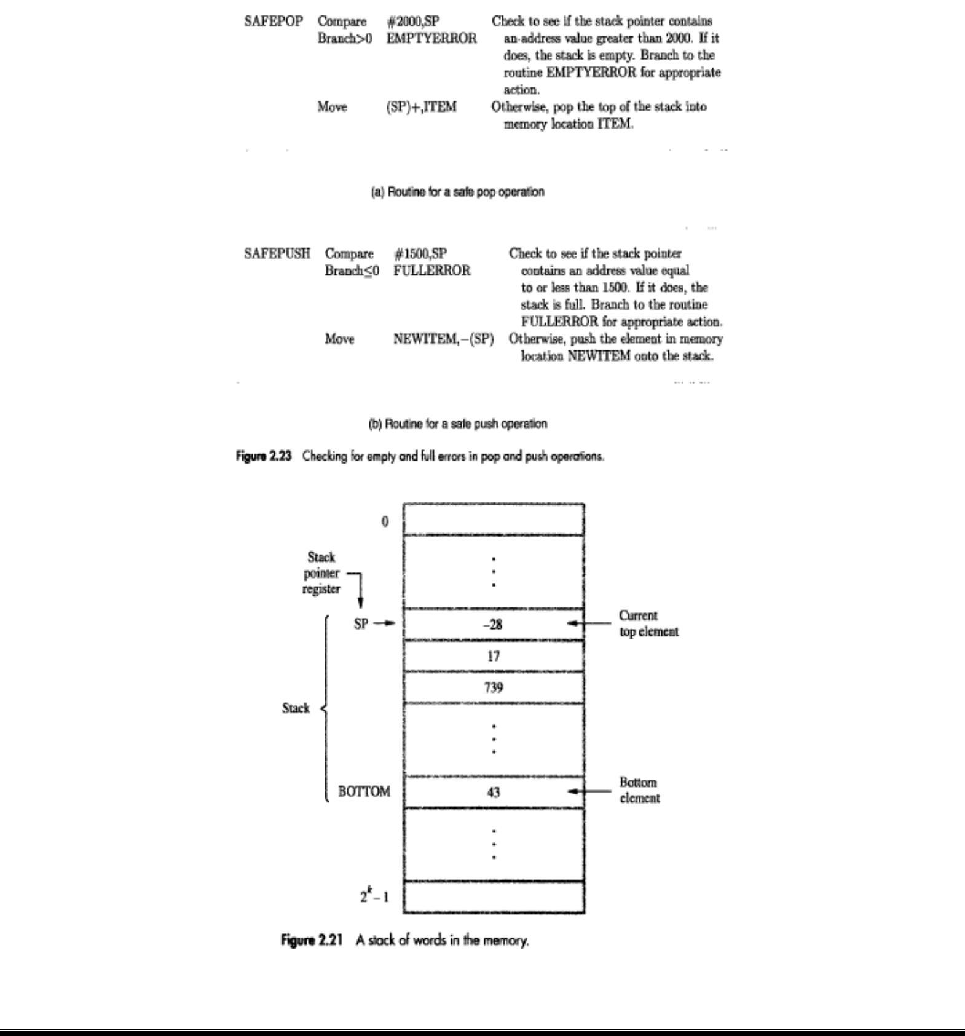
1.14 STACKS
• A stack is a list of data elements with the accessing restriction that elements can be added or removed at one end of the list only. This end is called the top of the stack, and the other end is called the bottom (Figure: 2.21).
• The terms push and pop are used to describe placing a new item on the stack and removing the top item from the stack, respectively.
• A processor-register is used to keep track of the address of the element of the stack that is at the top at any given time. This register is called the SP (Stack Pointer).
• If we assume a byte-addressable memory with a 32-bit word length,
→The push operation can be implemented as
Subtract #4,SR
Move NEWITEM,(SP)
→ The pop operation can be implemented as
Move (SP),ITEM
Add #4,SP
• Routine for a safe pop and push operation as follows
1.15 QUEUE
• Data are stored in and retrieved from a queue on a FIFO basis.
• Difference between stack and queue?
1) One end of the stack is fixed while the other end rises and falls as data are pushed and popped.
2) A single pointer is needed to point to the top of the stack at any given time.
On the other hand, both does of a queue move to higher addresses as data are added at the back and removed from the front. So, two pointers are needed to keep track of the two does of the queue.
3) Without further control, a queue would continuously move through the memory of a computer in the direction of higher addresses. One way to limit the queue to a fixed region in memory is to use a circular buffer.
1.16 SUBROUTINES
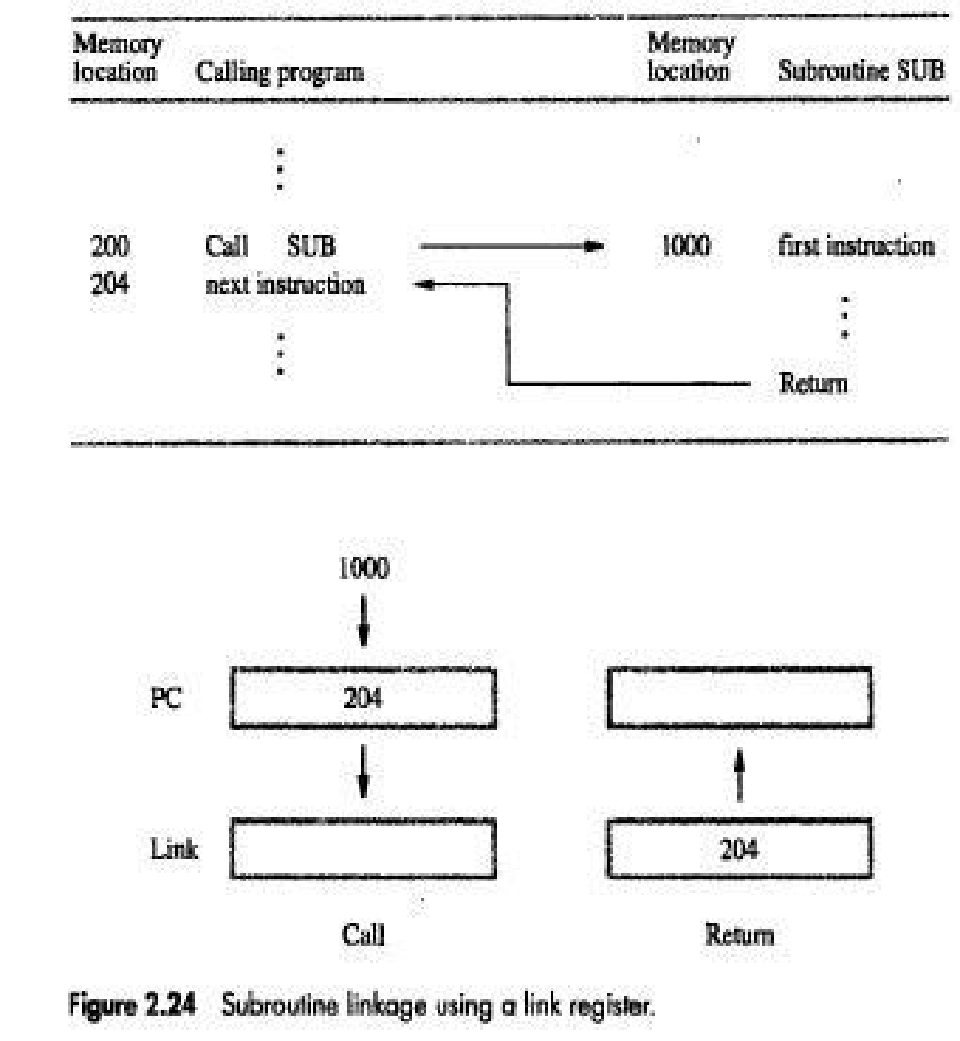
• A subtask consisting of a set of instructions which is executed many times is called a subroutine.
• The program branches to a subroutine with a Call instruction (Figure: 2.24).
• Once the subroutine is executed, the calling-program must resume execution starting from the instruction immediately following the Call instructions i.e. control is to be transferred back to the calling-program. This is done by executing a Return instruction at the end of the subroutine.
• The way in which a computer makes it possible to call and return from subroutines is referred to as its subroutine linkage method.
• The simplest subroutine linkage method is to save the return-address in a specific location, which may be a register dedicated to this function. Such a register is called the link register.
• When the subroutine completes its task, the Return instruction returns to the calling-program by branching indirectly through the link-register.
• The Call instruction is a special branch instruction that performs the following operations:
→ Store the contents of PC into link-register.
→ Branch to the target-address specified by the instruction.
• The Return instruction is a special branch instruction that performs the operation:
→ Branch to the address contained in the link-register.
1.16.1 SUBROUTINE NESTING AND THE PROCESSOR STACK
• Subroutine nesting means one subroutine calls another subroutine.
• In this case, the return-address of the second call is also stored in the link-register, destroying its previous contents.
• Hence, it is essential to save the contents of the link-register in some other location before calling another subroutine. Otherwise, the return-address of the first subroutine will be lost.
• Subroutine nesting can be carried out to any depth. Eventually, the last subroutine called completes its computations and returns to the subroutine that called it.
• The return-address needed for this first return is the last one generated in the nested call sequence. That is, return-addresses are generated and used in a LIFO order.
• This suggests that the return-addresses associated with subroutine calls should be pushed onto a stack. A particular register is designated as the SP(Stack Pointer) to be used in this operation.
• SP is used to point to the processor-stack.
• Call instruction pushes the contents of the PC onto the processor-stack.
Return instruction pops the return-address from the processor-stack into the PC.
1.16.2 PARAMETER PASSING
• The exchange of information between a calling-program and a subroutine is referred to as parameter passing (Figure: 2.25).
• The parameters may be placed in registers or in memory-location, where they can be accessed by the subroutine.
• Alternatively, parameters may be placed on the processor-stack used for saving the return-address • Following is a program for adding a list of numbers using subroutine with the parameters passed through registers.

1.16.3 STACK FRAME
• Stack frame refers to locations that constitute a private work-space for the subroutine (Figure:2.26).
• The work-space is
→ created at the time the subroutine is entered &
→ freed up when the subroutine returns control to the calling-program.
• Following is a program for adding a list of numbers using subroutine with the parameters passed to stack
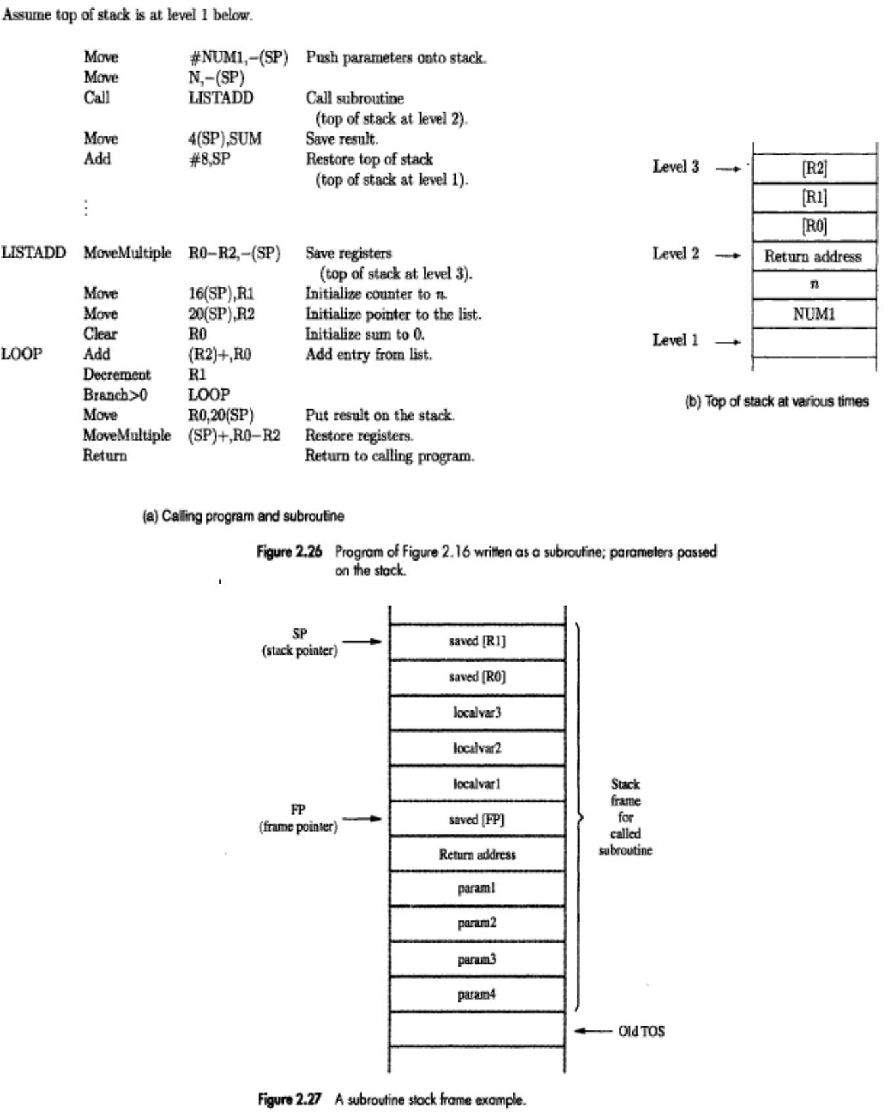
• Fig: 2.27 show an example of a commonly used layout for information in a stack-frame.
• Frame pointer (FP) is used to access the parameters passed to the subroutine &
to the local memory-variables
• The contents of FP remains fixed throughout the execution of the subroutine, unlike stack-pointer SP, which must always point to the current top element in the stack.
❖ Operation on Stack Frame
• Initially SP is pointing to the address of old TOS.
• The calling-program saves 4 parameters on the stack (Figure 2.27).
• The Call instruction is now executed, pushing the return-address onto the stack.
• Now, SP points to this return-address, and the first instruction of the subroutine is executed.
• Now, FP is to be initialized and its old contents have to be stored. Hence, the first 2 instructions in the subroutine are:
Move FP,-(SP)
Move SP,FP
• The FP is initialized to the value of SP i.e. both FP and SP point to the saved FP address.
• The 3 local variables may now be pushed onto the stack. Space for local variables is allocated by executing the instruction
Subtract #12,SP
• Finally, the contents of processor-registers R0 and R1 are saved in the stack. At this point, the stack-frame has been set up as shown in the fig 2.27.
• The subroutine now executes its task. When the task is completed, the subroutine pops the saved values of R1 and R0 back into those registers, removes the local variables from the stack frame by executing the instruction.
Add #12,SP
• And subroutine pops saved old value of FP back into FP. At this point, SP points to return-address, so the Return instruction can be executed, transferring control back to the calling-program.
❖ STACK FRAMES FOR NESTED SUBROUTINES
• Stack is very useful data structure for holding return-addresses when subroutines are nested.
• When nested subroutines are used; the stack-frames are built up in the processor-stack.
• Consider the following program to illustrate stack frames for nested subroutines (refer fig no. 2.28 from text book).
The Flow of Execution is as follows:
• Main program pushes the 2 parameters param2 and param1 onto the stack and then calls SUB1.
• SUB1 has to perform an operation & send result to the main-program on the stack (Fig:2.28& 29).
• During the process, SUB1 calls the second subroutine SUB2 (in order to perform some subtask).
• After SUB2 executes its Return instruction; the result is stored in register R2 by SUB1.
• SUB1 then continues its computations & eventually passes required answer back to main-program on the stack.
• When SUB1 executes return statement, the main-program stores this answers in memory-location RESULT and continues its execution.
❖ LOGIC INSTRUCTIONS
• Logic operations such as AND, OR, and NOT applied to individual bits.
• These are the basic building blocks of digital-circuits.
• This is also useful to be able to perform logic operations is software, which is done using instructions that apply these operations to all bits of a word or byte independently and in parallel.
• For example, the instruction
Not dst
❖ SHIFT AND ROTATE INSTRUCTIONS
• There are many applications that require the bits of an operand to be shifted right or left some specified number of bit positions.
• The details of how the shifts are performed depend on whether the operand is a signed number or some more general binary-coded information.
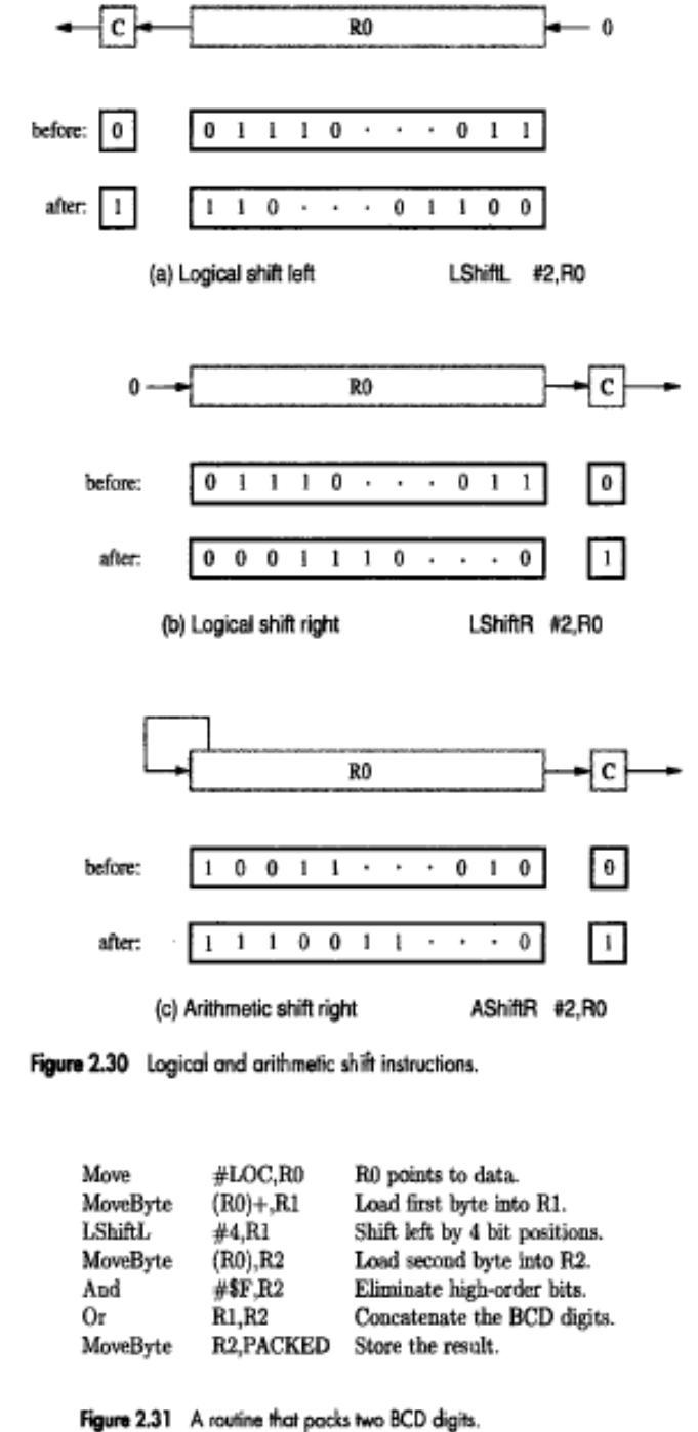
• For general operands, we use a logical shift.
For a number, we use an arithmetic shift, which preserves the sign of the number.
❖ LOGICAL SHIFTS
• Two logical shift instructions are needed, one for shifting left(LShiftL) and another for shifting right(LShiftR).
• These instructions shift an operand over a number of bit positions specified in a count operand contained in the instruction.
❖ ROTATE OPERATIONS
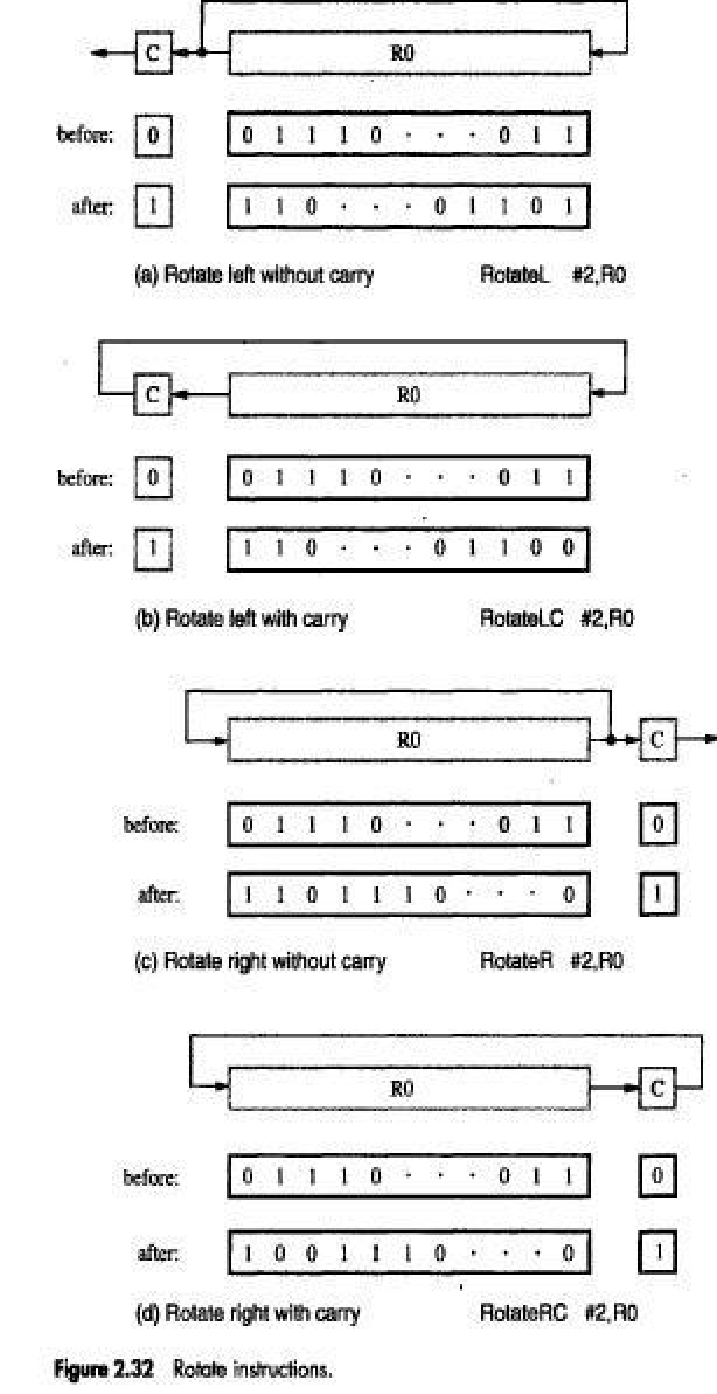
• In shift operations, the bits shifted out of the operand are lost, except for the last bit shifted out which is retained in the Carry-flag C.
• To preserve all bits, a set of rotate instructions can be used.
• They move the bits that are shifted out of one end of the operand back into the other end.
• Two versions of both the left and right rotate instructions are usually provided.
In one version, the bits of the operand are simply rotated.
In the other version, the rotation includes the C flag.
❖ Multiplication And Division:
Multiply Ri,Rj
Rj= [Ri]*[Rj]
Division Ri,Rj
Rj=[Ri]/[Rj]


