Thermal Engineering 1st Module

Thermodynamics: definition and scope

"Thermodynamics" is a term that is derived from Greek words theme and dynamics. Word theme means heat and dynamics means strength. Thus literally thermodynamics means heat strength or heat power. In other words, it means the process of converting heat into mechanical power. However, modern thermodynamics deals with more than just thermal energy.

Thermodynamics is defined as the science and technology that deals with the laws that govern the transformation of energy from one form to another form.

There are four laws of thermodynamics: the zeroth, first, second and third. These laws form the basis for all types of thermodynamic analysis

Scope

Thermodynamics is used in a wide range of science and engineering areas, including physical chemistry, biochemistry, chemical engineering, and mechanical engineering, as well as more sophisticated subjects like meteorology.

The study of chemical compounds and chemical reactions was significantly expanded after the initial application of thermodynamics to mechanical heat engines. Chemical thermodynamics investigates the function of entropy in chemical reactions and has contributed significantly to the field's growth and knowledge.

Classical thermodynamics uses macroscopic, quantifiable features to describe the states of thermodynamic systems in near-equilibrium. It is used to simulate energy, work, and heat exchanges using thermodynamic rules.

Thermodynamics is a discipline of science that studies the various types of energy, their quantitative correlations, and the energy changes that occur throughout physical and chemical processes.

Microscopic and Macroscopic approaches

Microscopic point of view considers that matter is composed of molecules. Each of these molecules have definite velocity and energy at a given instant. The velocity and energy change very frequently due to collisions of molecules.

Thus microscopic viewpoint might focus on molecules, atoms or even an electron and nucleus individually. Hence a complete description would require an enormous effort with suitable approximations.

The microscopic analysis or microscopic thermodynamics is also known as statistical thermodynamics because here, individual molecule is studied and the analysis is applied to collective molecular action by statistical methods.

Macroscopic point of view considers the effect of the action of many molecules instead of single molecules. For example, we measure distance in meters, time in seconds etc. These measurements are very large compared with the events on a microscopic or molecular level and hence the term macroscopic.

Classical thermodynamics is of macroscopic nature. The fundamental laws, or statements, deal only macroscopic properties of matter.

Comparison Chart

Engineering thermodynamics: definition, some practical applications of engineering thermodynamic.

THERMODYNAMIC SYSTEMS

A thermodynamic analysis involves the laws of thermodynamics applied to a thermodynamic system.

A thermodynamic system is a prescribed region of space or a finite quantity of matter. It is often referred to as just a system.

Basically there are three different types of systems.

Closed System

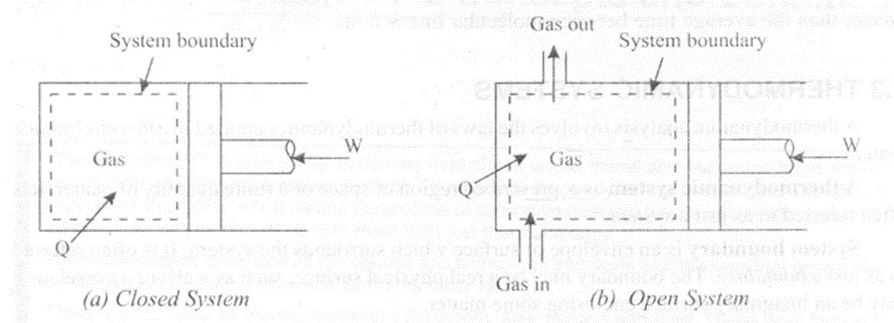
It is defined as the system of fixed content or matter (mass), in which only energy transfer takes place. Thus in a closed system, mass doesn't cross the system boundary even though energy may cross the system boundary

Consider figure 1.2 (a) in which the system consists of a gas confined between the piston and the cylinder. Even though heat and work may cross the boundary, and volume of the system may change due to the movement of the piston inside the cylinder, the system is said to be a closed system. This is because there is no flow of mass across the system boundary.

Open System

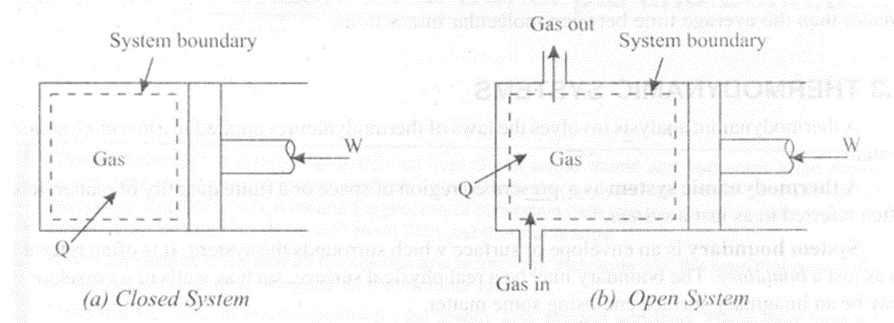
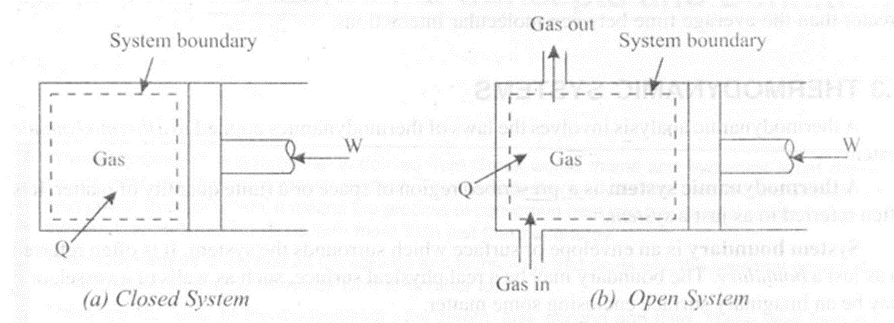
If matter flows into or out of a system, then the system is known as open system. Thus in an open system, both mass and energy may cross the system boundary. Consider figure 1.2 (b) in which a gas is compressed and expanded during the movement of a piston inside the cylinder. Here, in addition to heat and work, matter or mass may also cross the system boundary. Such a system is known as an open system

Isolated System

In an isolated system neither mass nor energy crosses the system boundary.

Consider a pan of water in a mass and energy impervious insulated box, thus forming an isolated system as shown in figure 1.3. Since the box is insulated there is absolutely no transfer of energy as well as matter or mass. Such a system is known as an isolated system.

Characteristics of system boundary

System boundary is an envelope or surface which surrounds the system. It is often referred to as just a boundary. The boundary may be a real physical surface, such as walls of a vessel, or it may be an imaginary surface enclosing some matter.

The system and the boundary are always chosen by an analyst and they are usually not specified in a problem statement. It may be noted that when different systems are used to analyze the same quantity, they should produce the same basic results in each case. A system and hence a boundary need not be fixed in space. They may move, deform, and increase or decrease in size with time.

Environment and Universe

The region outside the system boundary and contiguous to it is known as environment or the surroundings. The combined system and the environment are referred to as universe.

CONTROL VOLUME AND CONTROL SURFACE

A control volume is defined as a volume in space through which matter, momentum and energy may flow. It is bounded by a surface called control surface. A control volume can be fixed in size and shape, as in the case of a nozzle, or it may have a moving boundary, as shown in fig.

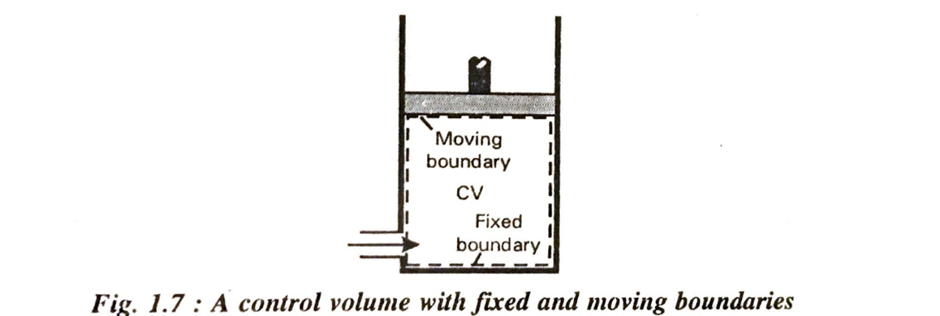
The control volume may be stationary or may be moving at a constant velocity.

If the control volume changes both in size and ill position, the control volume is equivalent to all open system. If no mass transfer occurs across the control surface, the control volume becomes identical with the closed system. The concept of control volume is useful in analysing the fluid flow. In the figure 1.4 the solid line represents the control surface and the dotted line represents system boundary

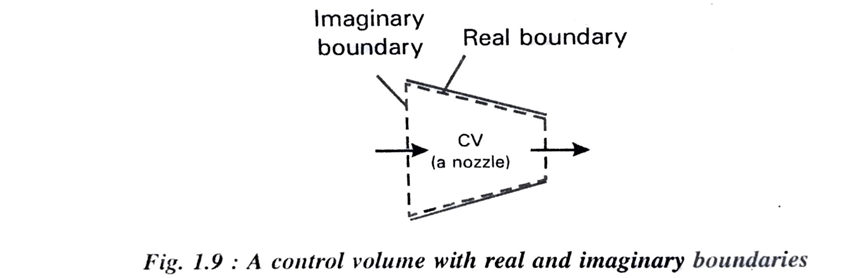
The boundaries of control volume is called control surface and the control surface can be real or imaginary. In  a nozzle the inner surface of the nozzle forms the real part of the boundary and the entrance and exit area from the imaginary part since there are no physical surface which exist there as shown in fig

Thermodynamic properties and state

The state of a system at any instant is its condition of existence at that instant. Consider a given mass of water. Initially it is in liquid form and if we heat it, it may become a vapour or if we cool it, it may become a solid. It can be noted that in each phase water may exist at different pressures and temperatures or in thermodynamic term, water may exist in Different states. Thus the state may be identified or described by certain observable, macroscopic properties like pressure p, temperature T, specific volume v, internal energy u, enthalpy h etc.

A property can be defined as any quantity that depends on the state of the system and is independent of the path by which the system has reached the given state.

The change in value of a property is thus fixed only by the end state of the system.

[n classical thermodynamics there are two different types of properties, intensive and extensive

Intensive property is defined as any thermodynamic property ofa system that is independent of the system mass. Examples are pressure, temperature, density and velocity.

Intensive mass based properties are symbolized by lower case letters, and intensive mole-based properties are symbolized by lower case letters with over bars. Thus v, ke, pe etc., are the symbols for mass based specific volume, kinetic energy, potential energy etc.

Extensive property is defined as any thermodynamic property of a system that depends on mass of the system. Examples are mass, volume and total energy.

Extensive properties are symbolized by upper case letters. Thus V, E, KE etc., are the symbols used for volume, total energy, kinetic energy etc. Some exceptions are temperature T (intensive property), mass m and number of moles n (extensive property).

Most extensive properties can be converted into intensive properties by dividing the extensive property by the system mass or the number of moles in the system. Intensive properties thus created are called specific properties. e.g.; specific volume, molar specific volume etc.,

THERMODYNAMIC PROCESSES AND CYCLES

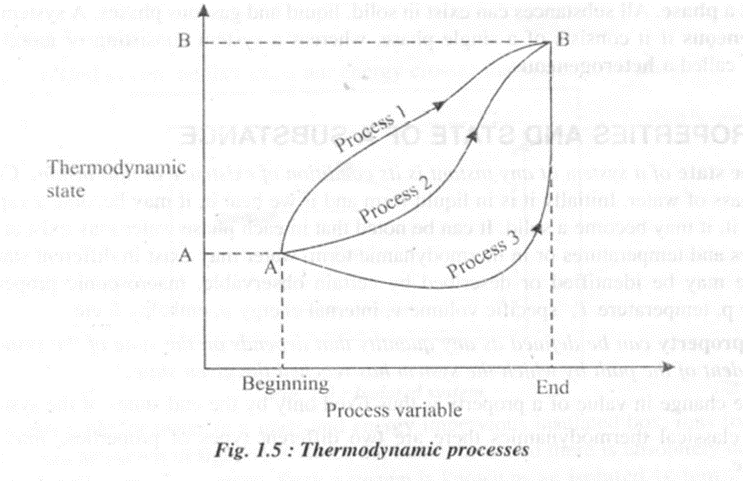
Thermodynamic process is defined as the path of the thermodynamic stales that a system passes through as it goes from all initial state to a final state. Thus, process is a transition in which a system changes from an initial state to a final state. If the process goes on so slowly that the state of equilibrium exists at every moment, then such a process is referred to as an equilibrium process, otherwise it is referred to as a non-equilibrium process. A process can change a system from one non equilibrium state to another by following a path of non-equilibrium states. Figure 1.5 shows three different processes following different paths.

Quasi static process

During a thermodynamic process to promote the change of state, it is necessary that some unbalanced potential must exist either within the system or between the system and the surroundings. When this unbalanced potential is very small, the system can be considered as infinitesimally close to the state of equilibrium at all times. This process is known as quasi-static process.

A quasistatic process is the one ill which the deviation from the thermodynamic equilibrium is infinitesimal. All the states the system passes through during a quasistatic process can be considered as equilibrium states. Consider a pressure PI of a gas on one face of a frictionless piston and a pressure p] on the opposite face. If the two pressures are equal, then the system is in equilibrium. If PI is infinitesimally larger than P2 ' the gas on side PI will undergo a small expansion as the piston moves; at the same time, the gases on both sides of the piston are essentially in equilibrium.

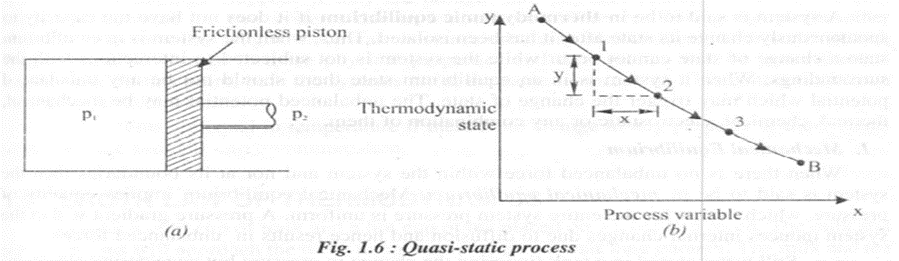
In the figure L6(b) AB represents a quasi-static process and at the successive states I, 2, 3 etc., the system is approximated to thermodynamic equilibrium. A thermodynamic cycle is the one ill which a system ill a given state goes through a number of different processes and finally returns to its initial state. Thus for a thermodynamic cycle the initial and final states remain identical. Steam which circulates through a steam power plant constitutes a steam cycle.

A reversible process is defined as the process that occurs in a reverse direction such that the initial state and all energies transferred or transformed during the process can be completely restored in both system and environment. Thus a reversible process doesn't leave any net change in the system or in the surroundings.

e.g. : Reversible adiabatic process.

An irreversible process is defined as the process that is not reversible. Thus, during an irreversible process the system and the surroundings are restored to their respective initial states with a net change in the system and in the environment. All the processes which involve dissipative effects are irreversible.

e.g. : Flow through pipes involving friction.

Thermodynamic equilibrium

A system is said to be in thermodynamic equilibriumif it does not have the capacity to spontaneously change its state after it has been isolated.

Thus, when the system is in equilibrium state a change of state cannot occur while the system is not subjected to interactions with the surroundings

1. Mechanical Equilibrium

When there is no unbalanced force within the system and nor at its boundaries then the system is said to be in mechanical equilibrium. Mechanical equilibrium implies equality of pre sure, which means for the entire system pressure is uniform. A pressure gradient within the system induces internal changes due to diffusion and hence results in unbalanced forces.

e.g., Still water stored in a tank (ignoring the change in pressure but considering elevation) due to gravitational force.

2. Chemical Equilibrium

When there is no chemical reaction or a process such as diffusion, the system is said to be in chemical equilibrium.

It can be noted that a system in mechanical equilibrium can undergo a change in its internal structure due to chemical reaction or diffusion of matter. Thus in chemical equilibrium there will be no mass diffusion in the system and also there will be no chemical reactions.

3. Thermal Equilibrium

When there is no temperature gradient within the system, the system is said to be in thermal equilibrium.

Consider a system which is in mechanical and chemical equilibrium. The system be separated by a diathermic wall which allows heat flow through it from the surroundings. If the temperature of the surroundings is higher, then heat flows from the surroundings towards the system. This results in increased temperature of the system. After sufficiently long period, both the system and the surroundings attain the same temperature and heat interaction between them ceases.

4. Electrical equilibrium

When there is no electrical potential gradient within a system, the system is said to be in electrical equilibrium.

5. Thermodynamic Equilibrium

When all the conditions of mechanical, chemical, thermal, electrical equilibrium are satisfied, the system is said to be in thermodynamic equilibrium. It is also known as an equivalent stare.

Statement of Zeroth law of thermodynamics. (No Numericals).

Consider a cold cup of milk and a hot cup of tea placed on a table in a room. The milk and tea in the cups will approach the room temperature when we wait long enough. The milk and tea are said to be in thermodynamic equilibrium with the room because we can sense that all of them are at the same temperature.

Now consider three thermodynamic systems A, B and C. If the system A is in thermal equilibrium with system C (i.e., A and C are at the same temperature) and system B is in thermal equilibrium with system C, then system A is in thermal equilibrium with system B. The above concept was introduced by R.H Fowler and E.A Guggenheim, which is known as Zeroth law of thermodynamics.

It states that, two bodies which are each ill thermal equilibrium with a third body, are ill thermal equilibrium with each other.

The zeroth law is the basis of the concept of temperature and is useful in comparing the temperature of two bodies A and B with the help of a third body C. This is done without actually bringing A and B in contact with each other. The test body C is known as a thermometer which defines equality of Temperature

Work and Heat:

Thermodynamic definition of work; examples, sign convention.

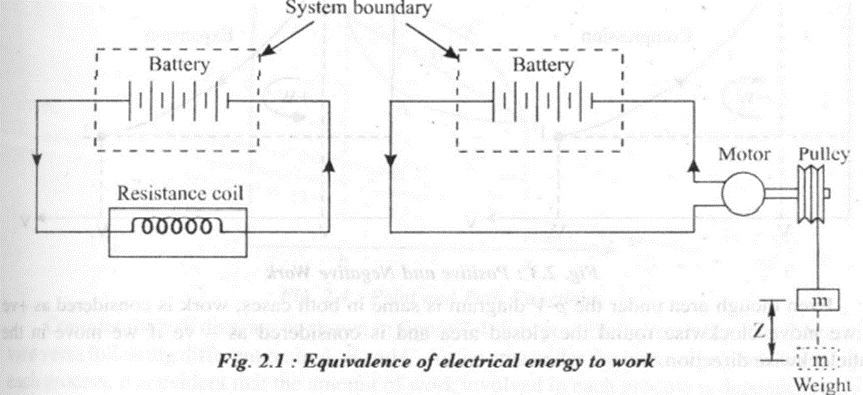
As defined in thermodynamics, work is the energy transfer across the system boundary in an organized manner such that its sole use could be reduced to lift a weight (mass) against gravitational effect

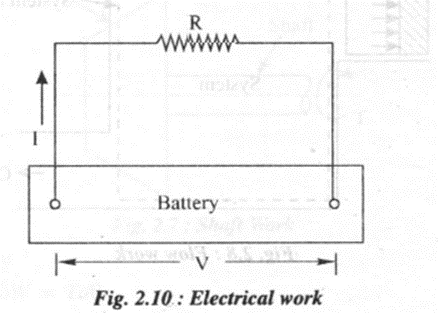
Consider for example, electrical energy from a storage battery crossing the system boundary as shown in the figure 2.1. When the switch is closed, current flows through the resistance coil which gets heated and thus heats the surrounding. Due to this action the charge on the battery (system) decreases. Even though there is interaction between the system and the surroundings, according to mechanics this can not be considered as work. This is because no force is acting through a distance.

Now imagine that the same electrical energy from the storage battery drives a motor which is coupled to a frictionless pulley, which in turn, raises a weight. Assuming that the net number of electrons carried by the electric wiring is zero, there is no net flow of mass across the system. Thus electrical energy is work.

SIGN CONVENTION FOR WORK

Work is considered as positive when work is done by the system and is considered as negative when work is done on the system. Thus, W denotes work done by the system and - W denotes work done on the system.

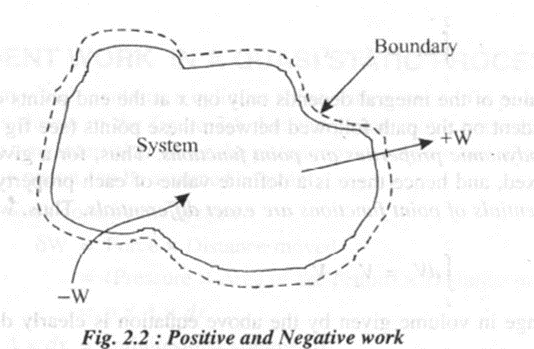
When the surroundings do + ve work, the system does an equivalent of - ve work, and vice versa. Thus for any process

W _system + W _surroundings = 0

Displacement work:

Consider a system which contains a cylinder, filled with a gas and a piston moving in the frictionless cylinder as shown in the figure 2.5. Let the piston move outward through a small distance dx (dx -> 0) in time interval dt. Since the piston moves only a small distance, the pressure acting on the face of the piston can be assumed constant.

The infinitesimal work done by the system

W = Force x Distance moved

= (Pressure x Area of the piston) x Distance moved,

=p x A x dx

But,

A x dx = Infinitesimal volume dV

Therefore,

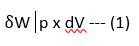
If the piston moves through a finite distance, the work done by the piston is obtained by integrating the 'above equation between the initial and final state. Thus

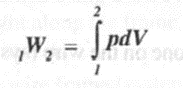
--(2)

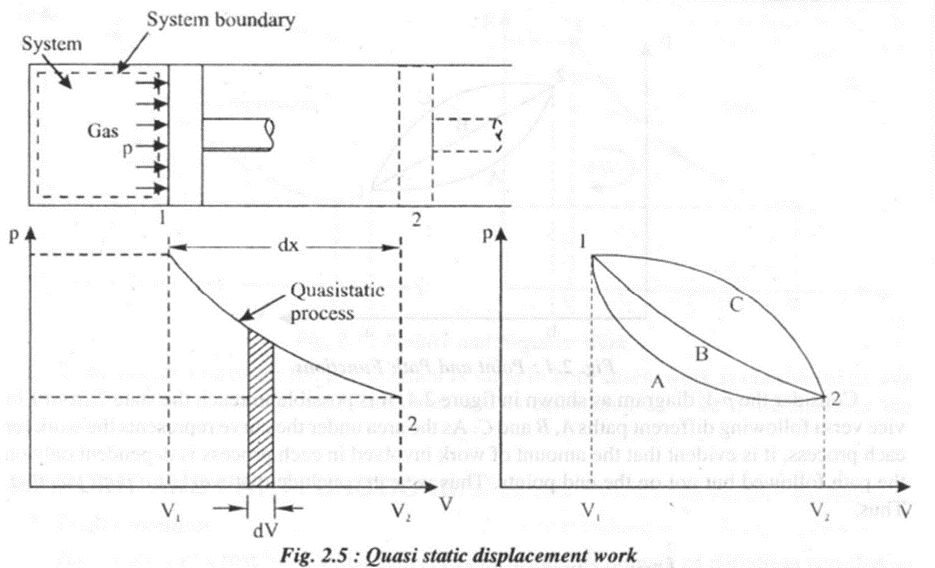
If the process proceeds from state 2 to state 1 we can write

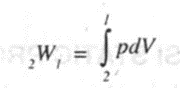
The above equations are applicable only for the following conditions.

• The process is reversible or frictionless or quasi static.

• The system is a closed system.

• The effect due to viscous force, magnetic, gravitational and electric current are negligible.

Other types of work

1.Stretching of a wire

Consider a wire of cross section A subjected to an external force of tension F. The length of the wire L changes to (L + dL) due to this action. Hence the infinitesimal work done is given by,

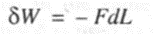
--- (I)

The negative sign indicates that work must be done on the wire (system) to effect a change in its length

2. Surface film

Consider a system consisting of a liquid film having a surface tension o as shown in the figure 2.6

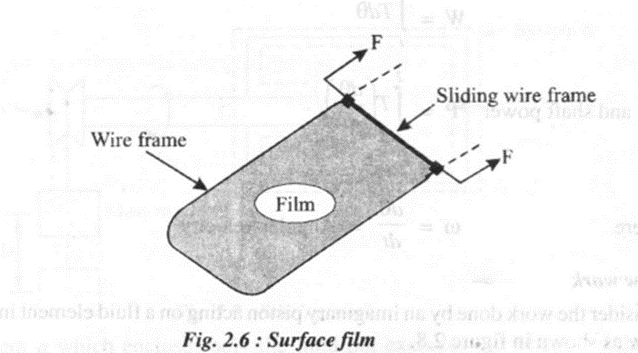
The film is maintained using a wire frame, one side of which is movable. When the sliding wire is moved left or right along the frame, work is done on or by the film.

During this movement area changes by an amount dA.

Work done by the wire frame (system) is given by,

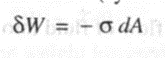
For' finite changes,

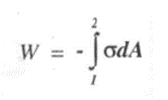
3.Shaft work

Consider an engine shaft rotated by means of an external force. The shaft undergoes an angular displacement when a constant torque T is applied to it.

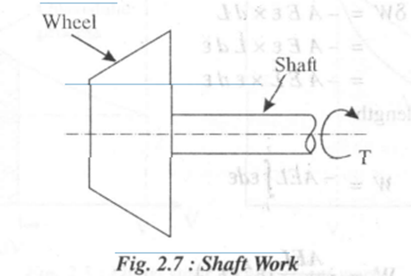
Shaft work is  given by

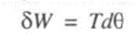
For finite changes, shaft work

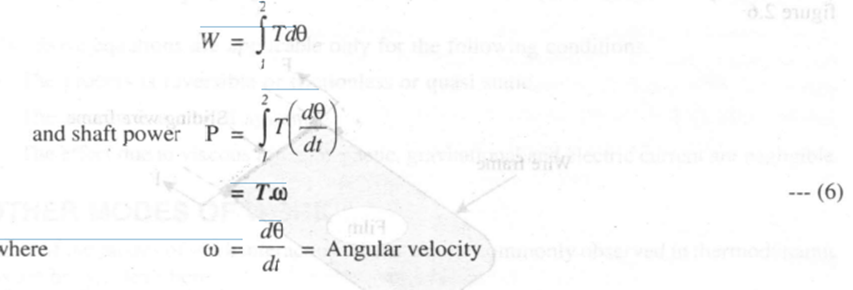
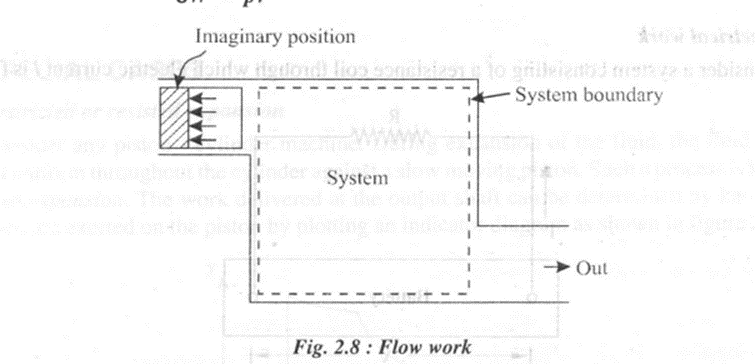
4. Flow work

Consider the work done by an imaginary piston acting on a fluid element in a process involving fluid flow as shown in figure 2.8.

The work done on this imaginary piston by the external pressure is given by

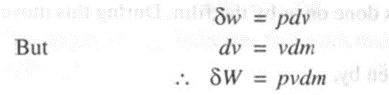
Since the above process involves simultaneous flow of fluid into and out of the system, we have for a fluid element entering the system,

5. Stirring work

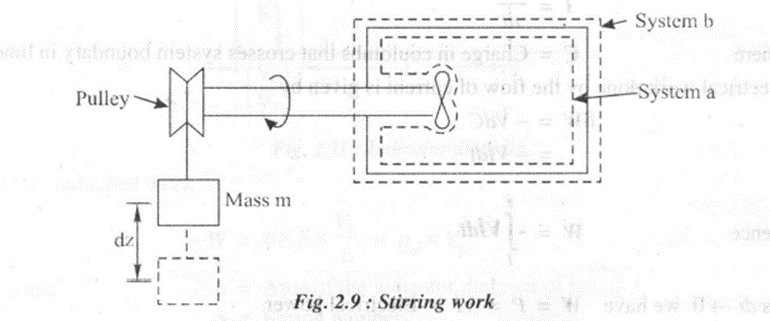
Consider system a which encloses only the fluid but excludes the wheel and the shaft as shown in figure 2.9. In this case both normal and.shear forces act on the wheel surface, But it is not possible to know distribution of force over the wheel surface and its variation with time exactly. Now consider the system boundary b which includes only shaft work in the boundary. In this case stirring work is given by,

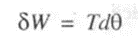
If m is the mass of the weight lowered through a distance dz, then

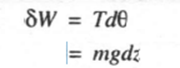
For finite variation we have

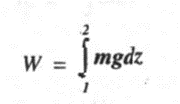
6. Electrical work

Consider a system consisting of a resistance coil through which electric current I is flowing

7. Magnetic Work

Consider a system which involves magnetic work. The work done in the magnetization of a paramagnetic substance is given by,

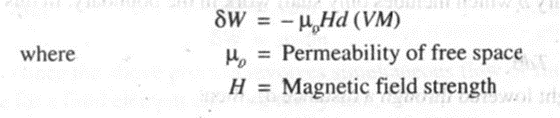
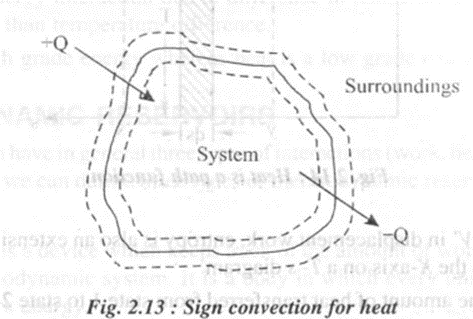
Heat; definition, units and sign convention

When two systems at different temperatures are placed in thermal contact with each other and isolated from all other systems, a change in temperature or other thermodynamic properties in both systems occur due to energy transfer.

The energy being transferred from one system to another system solely by reason of a temperature difference between the two systems is called heat.

The symbol Q is used to represent heat transfer to a system and q is used to represent heat transfer per unit mass of the system. As a convention of sign, heat transferred to a system is considered positive and heat transferred from a system is considered negative. In other words, Q is positive when surroundings have the higher temperature, and negative when the system is at higher temperature

Heat may not cause a temperature rise. For example, when heat is supplied to an ice-water mixture, the temperature of the mixture doesn't rise until all ice is melted. On the other hand, when there is an increase in temperature in a system it may not be solely due to heat transfer, it may be due to work transfer also.

A process in which heat doesn't cross the boundary of the system is called an adiabatic process. Thus in an adiabatic process there is only work interaction between the system and the surroundings.

A wall which is impermeable to heat flow is an adiabatic wall, whereas a wall which is permeable to heat flow is a diathermic wall.

Comparison of Work and Heat

Similarities

· Both work and heat are path functions. They are not the properties of the system and hence their differentials are inexact.

· Both work and heat exist during interactions only. They don't exist either before or after interactions. Heat may be present during a temperature rise or heat may not cause temperature rise.

· Both work and heat transfer occur across the system boundary and are always referred with reference to the system boundary.

· Heat, like work can never be a conserved fluid. Both heat and work of a system can be referred as transient energy. Hence it is improper to use the terms like 'heat contained', 'heat in' etc.,

Dissimilarities

· Work is a measure of organized and directed flow of energy whereas, heat transfer is a non-organized flow of energy of molecular and atomic interaction. However. These two forms of energy transfer are not equivalent.

· In case of work, the sole effect external to the system could be reduced to the raising of mass against gravity. In case of heat transfer other effects are also observed.

· Heat is the energy interaction due to difference in temperature whereas work is due to reasons other than temperature difference.

· Work is a high grade energy whereas heat is a low grade energy.