Thermal Engineering 5th Module

Thermal Engineering Mar 13, 2023

😁

Downloadable PDF at the end of the page

PART A

Forced Convections:

Applications of dimensional analysis for forced convection.

If the heat transfer by convection is assisted by some external means it is known as forced t, convection. The dimensional analysis for forced convection is correlated by

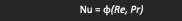
The forced convection heat transfer phenomenon can be influenced by the variables given in following table.

These seven variables are expressed in four primary dimensions (M,L,T) therefore, according to Buckingham pi theorem, the independent dimensionless group are:

= no. of variable affecting the phenomenon – No. of primary dimensions used.

Expressing the variable in their primary dimensions for π₁

π1=L^a(ML⁻³)^b(ML⁻¹T⁻¹)^c(MLT⁻³T⁻¹)d(LT⁻¹)

M⁰L⁰T⁰t⁰=M(^b+c+d)L(^{a−3b−c+d+1)}T^(−d)t^{(−c−3d−1)}

Separating the exponents for dimensional homogeneity

M=b+c+d=0

L=a-3b-c+d+1=0

T=-d=0

t=-c-3d-1=0

Solving these simultaneous equations, we get

D=0,c=-1,b=1,a=1

Hence the dimensionless group is formed is

π₁ =(Dρu_∞)/μ=Re_D(Reynolds number) Expressing the primary dimension for variables of π₂,

π₂=L^e(ML⁽⁻³⁾)^f(ML⁽⁻¹⁾)T⁽⁻¹⁾)^g(MLT⁽⁻³⁾T⁽⁻¹⁾)^h(L²T⁽⁻²⁾T⁽⁻¹⁾)¹

Separating the exponents for dimensional homogeneity.

M:0=f+g+h

L:0=e-3f-g+h+2

T:0=-h-1,

t:0=-g-3h-2

Solving these simultaneous equations, we get

H=-1,g=1,f=0,e=0

Hence the dimensionless group formed is,

π²= (μC_P)/k_f =Pr(Prandtl Number)

Expressing the primary dimension for variables for π₃

π₃ = L^e(ML⁽⁻³⁾)^f(ML⁽⁻¹⁾)T⁽⁻¹⁾)^g(MLT⁽⁻³⁾T⁽⁻¹⁾)^h(L²T⁽⁻²⁾T⁽⁻¹⁾)^l(MT⁽⁻³⁾T⁽⁻¹⁾)

M:0=j+k+l+1,

L:0=i-3j-k+l,

T:0=-l-1,

t: 0=-k-3l-3

Solving these simultaneous equations, we get

L=−1,k=0,j=0,i=1

Hence the dimensionless group formed is,

Significance of Dimension Analysis

1. It is helpful to check the dimensional homogeneity of any physical situation.

2 It is helpful to determine the dimensions of a physical quantity.

3 Dimensional homogeneity can be applied to units conversion from one system of units to other.

4. The qualitative solution brained by dimensional analysis can be converted into a quantitative result, determining any unknown constants experimentally.

Physical significance of Reynolds, Prandtl, Nusselt and Stanton numbers

1.Reynolds number

Reynolds number is defined as the ratio of inertia force to viscous force. When the Reynolds number is small the viscous forces are dominant whereas when Reynolds number is large, the inertia forces are more dominant

Thus,

Significance

Reynolds number is used to determine the change from laminar to turbulent flow as higher inertia forces result in small disturbances which amplify causing transition.

2.Prandtl number

Prandtl number is defined as the ratio of molecular diffusivity of momentum to the molecular diffusivity of heat. It represents the momentum and energy transport by the diffusion process.

Significance

The development of velocity and thermal boundary layers for flow along a flat pate and their magnitudes depend on the magnitude of Prandtl number.

3.Nusselt Number

Nusselt number is defined as the ratio of heat transfer by convection to conduction across the fluid layer of thickness L. A larger value of Nusselt nu,mber means heat transfer by convection is more

Significance

Nusselt number is a convenient measure of heat transfer coefficient. It relates convective surface coefficient h to thermal conductivity_k of the fluid

4.Stanton Number

Stanton number is defined as the ratio of heat flux to the fluid to the heat transfer capacity of the fluid flow.

5. Eckert Number

Eckert number is defined as the ratio of dynamic temperature due to fluid motion to the temperature difference

Significance

Itis an important dimensionless parameter which decides whether the viscous-energy-dissipation effects should be considered in the heat transfer analysis or not. If the Ecker number is small the viscous energy generation effects due to the motion of the fluid can be neglected as compared to the temperature differences involved in the heat transfer process.

6. Peclet Number

Peclet number is defined as the ratio of mass heat flow rate to the heat flow rate by conduction under a unit temperature gradient and through a thickness L

7. Graetz Number

Graetz number is defined as the ratio of the heat capacity of the fluid flowing through the pipe per unit length of the pipe to the conductivity of the pipe. It is significant only in heat flow to the fluid flowing through circular pipes. If D and L are diameter and length of the pipe respectively,

Then

8.Grashoff Number

Grashoff number is defined as the ratio of product of inertia force and-buoyance force to the square of viscous force.

Local Heat Transfer Coefficient

Heat-transfer coefficient at a particular point on the heat-transfer surface, equal to the local heat flux at this point (q_w) divided by the local temperature drop (Δt)

Drag Coefficient

When an object moves through a fluid, then to compute its resistance, the coefficient used is known as the Drag coefficient, denoted by C_d. The coefficient of drag is dimensionless, which is helpful in calculating aerodynamic drag and the impact of shape, inclination and conditions of flow in aerodynamics.

Basically, unsharpened and bulky objects will have a high drag coefficient, and streamlined objects will have a lower drag coefficient.

Where:

F_d denotes drag force (N)

ρ denotes density (kg/m³)

v denotes velocity (m/s²)

C_d denotes drag coefficient

A denotes the frontal area (m²)

PART B

Radiation Heat Transfer:

Thermal radiation-

If the radiation energy is emitted by bodies because of their temperature it is known as thermal radiation

Planck’s radiation law

Planck's law describes describes the spectral density of electromagnetic radiation emitted by a black body in thermal equilibrium at a given temperature T, when there is no net flow of matter or energy between the body and its environment.

Planck’s radiation law, a mathematical relationship formulated in 1900 by German physicist Max Planck to explain the spectral-energy distribution of radiation emitted by a blackbody (a hypothetical body that completely absorbs all radiant energy falling upon it, reaches some equilibrium temperature, and then reemits that energy as quickly as it absorbs it.

Planck’s law for the energy E_λ radiated per unit volume by a cavity of a blackbody in the wavelength interval λ to λ + Δλ (Δλ denotes an increment of wavelength) can be written in terms of Planck’s constant (h), the speed of light (c), the Boltzmann constant (k), and the absolute temperature (T):

The wavelength of the emitted radiation is inversely proportional to its frequency, or λ = c/ν

For a blackbody at temperatures up to several hundred degrees, the majority of the radiation is in the infrared radiation region of the electromagnetic spectrum. At higher temperatures, the total radiated energy increases, and the intensity peak of the emitted spectrum shifts to shorter wavelengths so that a significant portion is radiated as visible light

Wein’s displacement law.

Fig. 10-4 shows the variation of blackbody emissive power as a function of

at different values of T. From the figure it is clear that increasing the temperature , emmision of radiation i ncreases for a given wavelength and at any given temperature the emitted radiation varies with wavelength and reaches a peak. All the peaks tend to shift towards smaller wavelengths as the temperature increases.

The locus of these peaks is given by Wiens displacement law. It states that the product of maximum wavelength and aboslute temperature is a constant and is equal to 2897.6 µm.K. Thus the displacement of the maximum monochromatic emissive power is given by

Monochromatic emissive power of a black body is defined as the rate of energy emission per unit area at a particular wavelength

Stefan-Boltzman law

Stefan-Boltzman law states that the amount of radiant energy emitted per unit time from unit area or black surface is proportional to the fourth power of its absolute temperature

KIRCHOFF'S LAW

The absorplivity and emissivly of a body can be related by Kirchoff's law of radiation.

Consider a perfectly black enclosure which alsorbs all the incident radiation falling upon it as shown in Fig. 10-8. This enclosure will emit radiation according to the Stefan-Boltzman law. Let the radiant Tux arriving at some area in the enclosure be q, W/m². Suppose if the body is placed inside the enclosure and allowed to reach the equilibrium temperature with it. For this to happen there should not be an energy flow into or out of the body which would otherwise increase or lower its temperature. For equilibrium, the energy absorbed by the body must be equal to the energy

emitted.

effect of radiation Shield;

Heat transfer by radiation between two surfaces can be reduced effectively by inducing radiation shields which increase the surface resistance without removing any heat from the overall system. For effective insulation, it is possible to use many thin sheets of plastic coated with highly reflecting metallic films on both sides, separated by vacuum. Radiation shields are used in insulation of cryogenic storage tanks, thermometers, thermocouples etc.

Shielding between two surfaces reduces heat transfer significantly only if the shielding material is a low emissivity material. Shielding material placed between the two surfaces increases thermal resistance to radiation, reducing heat transfer rate. Thermal resistance increases if the emissivity of the material decreases.

Intensity of radiation and solid angle